A K. 610. feladat (2019. január)

K. 610. Három méter magasra vezető 1 méter széles tömör beton lépcsőt kell építenünk, egyforma magas lépcsőfokokkal. Minden lépcsőfoknak van egy magassága (\(\displaystyle m\)), és egy úgynevezett lépésmélysége (\(\displaystyle l\)), ahogy az ábra mutatja. A lépcsőfokoknál előírás, hogy \(\displaystyle 2m+l=64\) cm, valamint hogy a lépcsőfok ne legyen magasabb, mint amekkora a lépésmélysége. Legkevesebb hány lépcsőfokra lesz szükség? Mennyi betonra lesz szükség a minimális darabszámú lépcsőfokból álló lépcsőhöz?

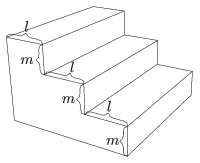
(6 pont)

A beküldési határidő 2019. február 11-én LEJÁRT.

Megoldás. Ha a lehető legmagasabb egy lépcsőfok, ami az előírásnak megfelel (ebből kell nyilván a legkevesebb), akkor \(\displaystyle 21\frac13\) cm magas, ezek lépésmélysége szintén \(\displaystyle 21\frac13\) cm. Viszont mivel csak egész számú lépcsőfok képzelhető el, csak a \(\displaystyle 300\) osztói adhatják a lépcsőfok magasságát, így az első szóba jövő magasság a \(\displaystyle 20\) cm, ahol a lépésmélység \(\displaystyle 24\) cm. Ebből \(\displaystyle 15\) darabra van szükség, ami a lehető legkevesebb.

A megfelelő betonmennyiséget kiszámíthatjuk, ha képzeletben a nyolcadik lépcsőfok felénél a talajjal párhuzamos síkkal kettévágjuk a lépcsőt, és a felső felét az alsóval összeillesztjük. Így egy téglatesthez jutunk, aminek magassága \(\displaystyle 1,5\) m, szélessége \(\displaystyle 1\) m, hossza \(\displaystyle 16\cdot0,24=3,84\) m, így térfogata \(\displaystyle 5,76~\textrm{m}^3\).

Statisztika:

147 dolgozat érkezett.
6 pontot kapott:	62 versenyző.
5 pontot kapott:	21 versenyző.
4 pontot kapott:	25 versenyző.
3 pontot kapott:	14 versenyző.
2 pontot kapott:	9 versenyző.
1 pontot kapott:	6 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	10 dolgozat.

A KöMaL 2019. januári matematika feladatai