 |
A K. 646. feladat (2020. január) |
K. 646. Van három gépünk, amelyek két-két bemenettel, és egy-egy kimenettel rendelkeznek. A gépek a bemeneteken keresztül megadott számokkal egy meghatározott műveletsort végeznek el, és ennek eredménye jelenik meg a kimeneten. A három gép tehát az ábra szerint néz ki.
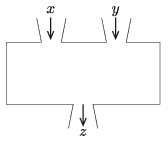
Az A gép kimenetén \(\displaystyle x\cdot y\) jelenik meg, a B gép kimenetén \(\displaystyle x^2+y\), a C gép kimenetén pedig \(\displaystyle 5\cdot x+3\cdot y\) (\(\displaystyle x\) és \(\displaystyle y\) jelöli az egyik, illetve a másik bemeneten beadott számokat). Összekötjük az A, B és C gépeket olyan módon, hogy az egyik kiválasztott gép egy-egy bemenetére a másik két gép kimenetét kötjük rá. Mennyi lesz az utolsó gépből kijövő lehető legnagyobb eredmény, ha a két első gépbe egyaránt az \(\displaystyle x=4\) és \(\displaystyle y=7\) értékeket tápláljuk be?
(6 pont)
A beküldési határidő 2020. február 10-én LEJÁRT.
Megoldás. Elvileg hat lehetőség van a gépek összekötésére, de ebből kettő azonos eredményt ad. A lehetőségek: 1) A bemeneteire kötjük B-t és C-t (ez sorrendfüggetlen a művelet szimmetriája miatt), 2) B bemeneteire kötjük A-t és C-t (két lehetőség), valamint 3) C bemeneteire kötjük A-t és B-t (ez is két lehetőség).
Az öt lehetőséget megvizsgálva megkapjuk a legnagyobb lehetséges kimeneteli értéket.
A betáplált számok nagyságát a kimenettel összefüggésben figyelembe véve a két-két esetből mindig az egyikben nyilvánvalóan nagyobb kimeneti érték lesz, és elég csak ezt vizsgálni.
Az adott \(\displaystyle x\) és \(\displaystyle y\) értékek esetén a három gép (A, B és C) kimeneti értéke: \(\displaystyle xy=28\); \(\displaystyle x^2+y=23\) és \(\displaystyle 5x+3y=41\).
Az 1) lehetőségben a kimeneti érték: \(\displaystyle 23\cdot41=943\); a 2) lehetőségben a kétfajta gép kimeneti értéke: \(\displaystyle 28^2+41<41^2+28=1709\); végül a 3) lehetőségben a kimeneti értékek: \(\displaystyle 5\cdot23+3\cdot28<5\cdot28+3\cdot23=209\).
Tehát a lehető legnagyobb eredmény, amit kaphatunk az \(\displaystyle 1709\).
Statisztika:
145 dolgozat érkezett. 6 pontot kapott: 102 versenyző. 5 pontot kapott: 3 versenyző. 4 pontot kapott: 6 versenyző. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 10 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 11 versenyző. Nem versenyszerű: 2 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2020. januári matematika feladatai
