A K. 647. feladat (2020. január)

K. 647. Egy papírból készült ikozaédert néhány él mentén felvágunk úgy, hogy széthajtva a test valamelyik (síkban fekvő) hálójához jussunk. Hány élt kell felvágni ehhez?

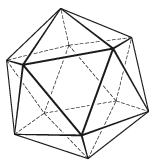
(6 pont)

A beküldési határidő 2020. február 10-én LEJÁRT.

Megoldás. Az ikozaédernek 20 háromszöglapja (mind szabályos háromszög) és 30 éle van. (Ez az ábráról leolvasható, vagy kiszámolható az alábbi gondolatmenettel: a 20 lapnak összesen 60 éle van, de minden él két lap találkozásánál található, így az élek száma 60:2=30.)

Az ikozaéder minden csúcsában öt háromszög csatlakozik. Emiatt a síkba terített hálójában egy csúcs körül legfeljebb öt háromszög lehet, hiszen ha több lenne, akkor nem lehetne oktaédert hajtani az alakzatból (hatnál több persze eleve nem is lehetne, hiszen \(\displaystyle 6\cdot60^{\circ}=360^{\circ}\)).

Így a hálót felépíthetjük valamelyik ,,szélső" háromszögtől kezdve, rendre egy-egy háromszög hozzáillesztésével valamelyik oldalhoz. 20 háromszög van, így 19 illesztés lesz. Tehát egy ikozaéder bármelyik hálója 20 háromszögből áll, melyek 19 oldal (él) mentén csatlakoznak egymáshoz. Így minden esetben \(\displaystyle 30 - 19 = 11\) élt kell felvágni.

Megjegyzés. A sok 3 pontos dolgozat annak köszönhető, hogy sokan egy konkrét testhálóra bizonyították az állítást, holott nem csak egyfajta testháló létezik.

Statisztika:

104 dolgozat érkezett.
6 pontot kapott:	Abonyi Bence, Ámon Benedek, Besze Zsolt, Fehér Anna, Fekete Patrik, Ferencz Mátyás, Gál Csaba, Gardev Dániel, Hajós Balázs, Hangodi Hajnalka, Hartmann Botond, Karádi Virág, Kedves Benedek János, Kiss-Beck Tamara, Kovács 212 Sára, Nagy László Zsolt, Ökördi Laura, Pekk Márton, Slézia Dávid, Szirtes Hanna, Szittyai Anna, Wodala János, Zsuffa Móric.
5 pontot kapott:	Ágoston Barbara, Árok Anna, Deme Erik, Fürész Tibor, Jójárt Emese, Morvai Eliza, Nagy 999 Csanád, Szittya Marcell Kristóf, Tóth Gréta, Zupkó Bence Kristóf.
4 pontot kapott:	5 versenyző.
3 pontot kapott:	43 versenyző.
2 pontot kapott:	9 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	5 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2020. januári matematika feladatai