A K. 648. feladat (2020. január)

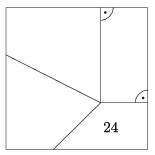
K. 648. Egy négyzet belső pontját összekötöttük minden oldalon az egyik oldalharmadoló ponttal az ábra szerint, és így négy négyszöget kaptunk. Ismerjük az egyik ilyen négyszög területét (lásd az ábrát). Határozzuk meg a többi négyszög területét.

(6 pont)

A beküldési határidő 2020. február 10-én LEJÁRT.

Megoldás. Használjuk az ábra jelöléseit. Tudjuk, hogy a jobb alsó trapéz területe 24: $\displaystyle t_4=\frac{(x+2x)\cdot x}{2}=24=\frac{3x^2}{2}$, vagyis $\displaystyle 48=3x^2$, amiből $\displaystyle 16=x^2$ és így $\displaystyle x=4$.

$\displaystyle t_1=x\cdot2x=4\cdot8=32,$

$\displaystyle t_2=\frac{(x+2x)\cdot2x}{2}=2\cdot\frac{(x+2x)\cdot x}{2}=2\cdot24=48,$

$\displaystyle t_3=(3x)^2-(t_1+t_2+t_3)=12^2-(24+32+48)=144-104=40.$

Statisztika:

168 dolgozat érkezett.
6 pontot kapott:	131 versenyző.
5 pontot kapott:	7 versenyző.
4 pontot kapott:	7 versenyző.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	4 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	6 dolgozat.

A KöMaL 2020. januári matematika feladatai