A K. 650. feladat (2020. február)

K. 650. Az ábrán látható kis négyzet oldala 3 cm, a nagy téglalap oldalai egész számok, és az egyik 2 cm-rel hosszabb a másiknál. A téglalap és a négyzet oldalai párhuzamosak, középpontjuk egybeesik. A satírozott terület úgy keletkezett, hogy a kis négyzet oldalait meghosszabbítottuk az egyik irányba, és ahol a nagy téglalap oldalait ezek elmetszették, azokat a pontokat kötöttük össze. Lehet-e a satírozott terület nagysága (cm$\displaystyle {}^2$-ben mérve) páros szám?

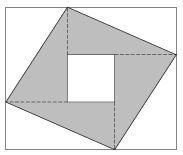
(6 pont)

A beküldési határidő 2020. március 10-én LEJÁRT.

Megoldás. Jelölje a téglalap oldalait $\displaystyle x$ és $\displaystyle x+2$. A satírozott terület nagysága $\displaystyle \frac{x(x+2)-9}{2}$, ha ez páros, akkor $\displaystyle x(x+2)-9$-nek 4-gyel oszthatónak kell lennie. Mivel $\displaystyle x$ és $\displaystyle x+2$ azonos paritású, ezért $\displaystyle x$ páratlan kell legyen. $\displaystyle x(x+2)-9=x^2+2x+1-10=(x+1)^2-10$. Ha $\displaystyle x$ páratlan, akkor $\displaystyle x+1$ páros, ekkor a négyzete osztható 4-gyel, de ha kivonunk belőle 10-et, akkor már nem osztható 4-gyel. Így nem lehet páros a satírozott terület nagysága.

Statisztika:

124 dolgozat érkezett.
6 pontot kapott:	62 versenyző.
5 pontot kapott:	9 versenyző.
4 pontot kapott:	5 versenyző.
3 pontot kapott:	5 versenyző.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	12 versenyző.
0 pontot kapott:	11 versenyző.
Nem versenyszerű:	6 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	6 dolgozat.

A KöMaL 2020. februári matematika feladatai