A K. 660. feladat (2020. szeptember)

K. 660. Az ábrán látható négyzeteket kitöltöttük az 1, 2, 3, 4, 5, 6, 7, 8 és 9 számokkal, majd a négyzetek közötti körökbe beírtuk mindenhol a két szomszédos négyzetbe írt szám összegét. Ezután néhány körből a benne lévő számot kiradíroztuk, a négyzeteket pedig besatíroztuk.

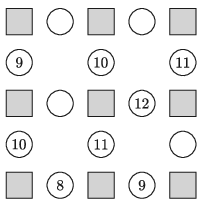
$\displaystyle a)$ Melyik számokat radíroztuk ki az üres körökből?

$\displaystyle b)$ Írjuk be mindegyik négyzetbe azt a számot, amit eredetileg beleírtunk.

(6 pont)

A beküldési határidő 2020. október 12-én LEJÁRT.

Megoldás. $\displaystyle a)$ A felső sorban a jobb oldali üres körben 9-es van, mert ha a jobb felső négy négyzet közé a körökbe írt számokat tekintjük, akkor a szemköztiek összege egyenlő kell, hogy legyen, hiszen $\displaystyle (a+b)+(c+d)=(a+d)+(b+c)$.

Hasonlóképpen a jobb oldali oszlop üres körébe $\displaystyle 12+9-11=10$ kerül, a középső sor üres körébe $\displaystyle 10+11-8=13$, illetve a felső sor üres körébe pedig $\displaystyle 9+10-13=6$. Tehát a kiradírozott számok sorban (balról jobbra, fentről lefelé): 6, 9, 13, 10.

$\displaystyle b)$ A 6 kétféleképpen áll elő két különböző pozitív egész szám összegeként ($\displaystyle 1+5$, $\displaystyle 2+4$), mindkét esetben kétféle sorrendben lehet beírni a számokat.

Ha 1-5-öt írunk be, akkor a felső sor (balról jobbra, ezután is mindig): 1, 5, 4 a középső sor: 8, 5, 7, ami nem lehet, mert így két 5-ös lenne.

Ha 5-1-et írunk be, akkor a felső sor: 5, 1, 8 a középső sor: 4, 9, 3, az alsó sor pedig: 6, 2, 7, ami megfelelő kitöltés.

Ha 2-4-et írunk be, akkor a felső sor: 2, 4, 5, a középső sor: 7, 6, 6, ami nem jó, mert két 6-os nem lehet.

Ha 4-2-t írunk be, akkor a felső sor 4, 2, 7, a középső sor: 5, 8, 4, az alsó sor pedig 5, 3, 6, ami nem megfelelő, mert két 5-ös van benne.

Tehát egy lehetséges kitöltés van: a felső sor: 5, 1, 8 a középső sor: 4, 9, 3, az alsó sor pedig: 6, 2, 7.

Statisztika:

218 dolgozat érkezett.
6 pontot kapott:	79 versenyző.
5 pontot kapott:	25 versenyző.
4 pontot kapott:	17 versenyző.
3 pontot kapott:	18 versenyző.
2 pontot kapott:	54 versenyző.
1 pontot kapott:	14 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	11 dolgozat.

A KöMaL 2020. szeptemberi matematika feladatai