A K. 679. feladat (2021. január)

K. 679. Peti még 3 éves korában kapta meg hat darabból álló építőjátékát, melyben minden építőelem téglatest alakú. Az elemek mérete \(\displaystyle 1~ \mathrm{dm} \times 1~ \mathrm{dm} \times 2~ \mathrm{dm}\). A tartódoboz belső mérete \(\displaystyle 3~ \mathrm{dm} \times 2~ \mathrm{dm} \times 2~ \mathrm{dm}\) és minden oldala más színű. Hányféle különböző elrendezésben pakolhatja be Peti a hat elemet a dobozába, ha az építőelemek ugyanolyan színűek és nem különböztetjük meg őket? (A dobozból nem lóghat ki egy építőelem sem.)

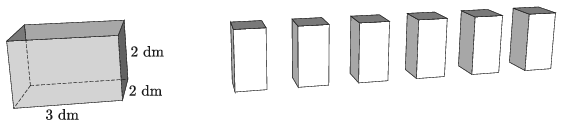
(6 pont)

A beküldési határidő 2021. február 15-én LEJÁRT.

Megoldás. Nevezzük álló elemnek az olyan építőelemet, ami az \(\displaystyle 1\times1\)-es lapjával a doboz alján áll. Az álló elemek száma 0, 2, 4 vagy 6 lehet. Páratlan sok álló elem azért nem lehet, mert akkor például a felső rétegben ez a páratlan sok álló elem páratlan sok köbdeciméternyi helyet hagy üresen, amit nem lehet kitölteni 2 köbdeciméter térfogatú (1 dm \(\displaystyle \times\) 1 dm \(\displaystyle \times\) 2 dm méretű) elemekkel.

Hat álló elemet elhelyezni egyféleképpen lehet.

Négy álló elemet elhelyezni most csak úgy lehet, hogy a felső és az első rétegben megmaradó 2-2 köbdeciméter térfogatú részt egy-egy nem álló elemmel ki lehessen tölteni. Ezt hétféleképpen tehetjük meg. A dobozt felülnézetben mutatja az ábra, a színes négyzetek jelzik az álló elemeket. A többi két elem elhelyezése egyértelmű.

Két álló elemet elhelyezni a fentieket figyelembe véve 9-féleképpen lehet.

Az első két esetben egymástól függetlenül 2-2 módon lehet elhelyezni a maradék építőelemeket az alsó és a felső rétegben, ami így 4-4 lehetőséget ad, a többi esetben egyértelmű az elhelyezés, így ez összesen 15 lehetőség.

Ha nincs álló elem, akkor az alsó és a felső rétegben három-három építőelem helyezkedik el.

Egy-egy ilyen rétegben a három elem három elrendezésben lehet.

Így a két rétegben 3 \(\displaystyle \cdot \) 3 \(\displaystyle =\) 9 elrendezés van.

Összesen tehát 1 \(\displaystyle +\) 7 \(\displaystyle +\) 15 \(\displaystyle +\) 9 \(\displaystyle =\) 32 lehetőség van az építőelemek visszapakolására.

Statisztika:

110 dolgozat érkezett.
6 pontot kapott:	Árvai Benedek, Bacsek Emma Borbála, Bakurek Máté, Barta Veronika, Biró Anna, Biró Róza, Buday Noémi, Érdi Ferenc Vince, Fórizs Emma, Gulyás Janka, Heim Flóra, Horváth 221 Zsóka, Laczó Dávid, Lajos Luca, Laskai Botond, Markovics Áron, Markovics Benjámin, Mayer Krisztián, Mészáros Ádám, Molnár Kristóf, Nagy 123 Krisztina, Németh Máté, Nyikos Botond Tamás, Richlik Márton, Sándor Eszter, Schäffer Donát, Sebestyén József Tas, Simon Géza, Solymosi Csongor, Susán Henrik, Tatár Bálint, Tomesz László Gergő, Török Hanga, Varga 621 Emese , Várhegyi Hajnal Eszter.
5 pontot kapott:	Gaspari Márton Samu.
4 pontot kapott:	13 versenyző.
3 pontot kapott:	29 versenyző.
2 pontot kapott:	10 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	8 versenyző.
Nem versenyszerű:	5 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2021. januári matematika feladatai