A K. 781. feladat (2023. október)

K. 781. Egy piros és egy zöld \(\displaystyle 2\times3\)-as táblázat mezőibe beírjuk az \(\displaystyle 1\), \(\displaystyle 2\), \(\displaystyle 3\), \(\displaystyle 4\), \(\displaystyle 5\), \(\displaystyle 6\) számokat úgy, hogy egy táblázaton belül minden szám pontosan egyszer szerepel. Összeadjuk a táblázatok megfelelő mezőiben álló számokat, így kapjuk a harmadik táblázatot. Az alábbiakban látunk egy példát.

Az alábbi ábrán látható piros és zöld üres táblázatot töltsük ki úgy, hogy az összeadás után a jobb oldali táblázatot kapjuk, amelynek jobb alsó sarkát letakartuk. Adjuk meg az összes megoldást.

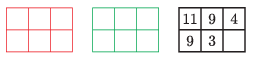
(5 pont)

A beküldési határidő 2023. november 10-én LEJÁRT.

Megoldás. Az összegtáblázat hiányzó száma a \(\displaystyle 6\), mert \(\displaystyle (1+2+3+4+5+6)\cdot2-(11+9+4+9+3)=6\).

A \(\displaystyle 11\) lehet \(\displaystyle 6+5\) vagy \(\displaystyle 5+6\), a két \(\displaystyle 9\) pedig ennek megfelelően \(\displaystyle 3+6\) vagy \(\displaystyle 6+3\), illetve \(\displaystyle 5+4\) vagy \(\displaystyle 4+5\). (Ez négy esetet ad, amit a szürke mezők kitöltése ad.) A \(\displaystyle 4\) nem lehet \(\displaystyle 2+2\), mert akkor a \(\displaystyle 3\)-at nem tudnánk felírni. Így pedig a további \(\displaystyle 3\)–\(\displaystyle 3\) mező kitöltése már adódik.

Négy lehetőség van.

Statisztika:

153 dolgozat érkezett.
5 pontot kapott:	Bencze Anna Borbála, Farkas Simon, Fülöp Magdaléna, Gyerkó Anna, Hajnal Ákos Huba, Hegedűs Gergely, Hornyák Zalán Zétény, Juhász Aliz, Juhász Zsombor, Kámán-Gausz Péter, Kőhidi Kata, Németh Ábel, Olajos Anna, Papp Emese Petra, Pázmándi Renáta , Schmidt Marcell, Sipos Levente, Szabó Máté, Szalóki Árpád, Tamás Attila Gábor, Tóth Luca, Varga Eliza, Viczián Adél.
4 pontot kapott:	Csáki Anikó, Doszpoly Zsombor, Dömők Bernadett, Ferencsik Domonkos, Gaál Gergely, Gáti Benjamin, Jiang Yufei, Kapiller Ákos Péter, Klučka Dominika, Kóródy Vera, Kriston Regő Márton, Kubica Ádám, Piller Zsófia, Sárvári Vanda, Timár Vince , Válek Péter, Zámbori Anna.
3 pontot kapott:	15 versenyző.
2 pontot kapott:	18 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	4 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	65 dolgozat.

A KöMaL 2023. októberi matematika feladatai