A K. 796. feladat (2024. január)

K. 796. Melyik síkidom területe a nagyobb?

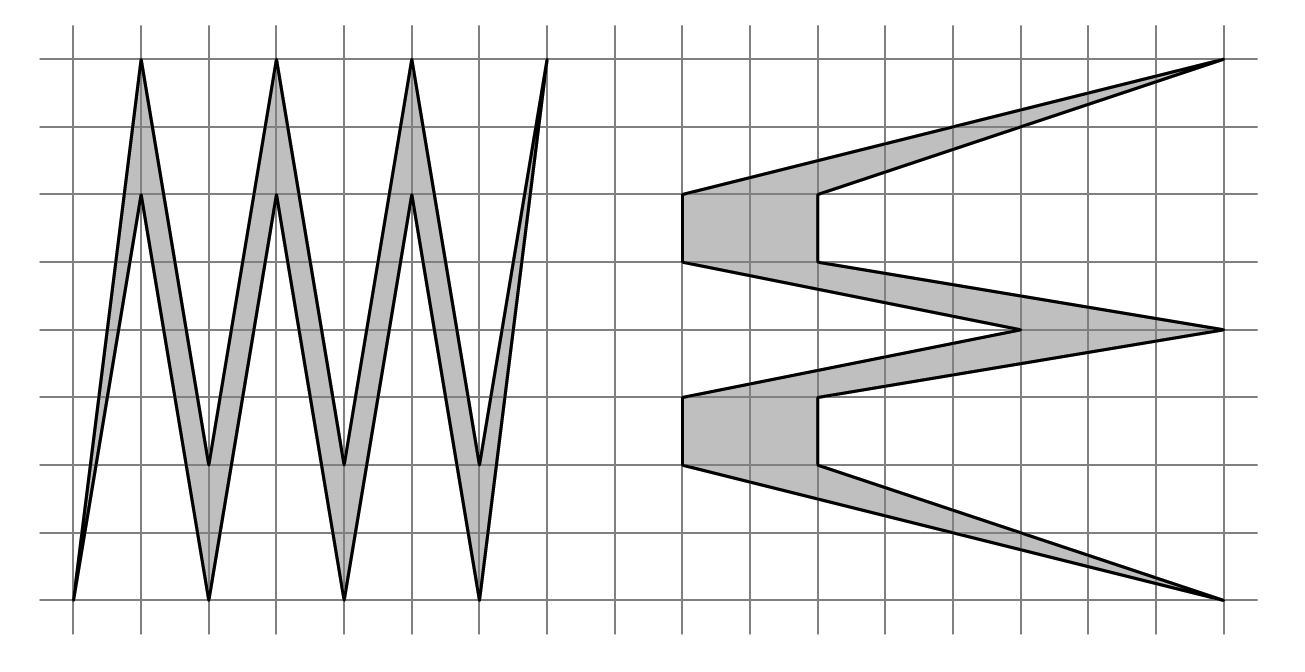
(5 pont)

A beküldési határidő 2024. február 12-én LEJÁRT.

1. megoldás.

Az első síkidom területe: \(\displaystyle 56-6 \cdot 6-2\cdot4=12\).

A második síkidom területe: \(\displaystyle 64-4\cdot6-2\cdot8-2\cdot3-5=13\). A második síkidom területe nagyobb.

2. megoldás.

Háromszögekre, paralelogrammákra, illetve trapézokra bontjuk a síkidomokat.

Az első síkidom területe: \(\displaystyle 5\cdot2+2\cdot1=12\).

A második síkidom területe: \(\displaystyle 4\cdot2+2\cdot2,5=13\). A második síkidom területe nagyobb.

Statisztika:

109 dolgozat érkezett.
5 pontot kapott:	Araguas Mátyás, Chen Peidong, Csáki Anikó, Dienes Csenge, Dömők Bernadett, Ferencsik Domonkos, Fülöp Magdaléna, Gaál Gergely, Gyerkó Anna, Hajnal Ákos Huba, Hegedűs Gergely, Hornyák Zalán Zétény, Ivák László, Juhász Gergely, Juhász Zsombor, Kapiller Ákos Péter, Kriston Regő Márton, Li Yujin, Máté Kristóf, Olajos Anna, Ördög Dominik, Pázmándi Renáta , Péterfia Kamilla, Piller Zsófia, Pivárcsik Márk, Sajó Marcell 16, Szabó Máté, Szedmák Szabrina, Szőke János, Tamás Attila Gábor, Timár Vince , Tóth Bálint Levente, Tóth Luca, Ungár Vince, Viczián Adél.
4 pontot kapott:	17 versenyző.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	45 dolgozat.

A KöMaL 2024. januári matematika feladatai