A K. 804. feladat (2024. március)

K. 804. Egy focimérkőzés végeredménye \(\displaystyle 4:3\) lett a hazai csapat javára. Hányféleképpen alakulhatott ki ez a végeredmény, ha volt olyan időszaka a mérkőzésnek, amikor a vendégcsapat vezetett?

(5 pont)

A beküldési határidő 2024. április 10-én LEJÁRT.

1. megoldás Jelöljük a hazai gólokat \(\displaystyle H\)-val, a vendéggólokat \(\displaystyle V\)-vel, és amikor gól esik, akkor írjuk le a megfelelő betűt, majd a következő gólnál újabb betűt írunk az előző mögé. Mivel a végeredmény \(\displaystyle 4:3\) lett, ezért \(\displaystyle 4\) darab \(\displaystyle H\) és \(\displaystyle 3\) darab \(\displaystyle V\) betűt írunk le sorban egymás mellé. Ezek közül azok jók, amikor van olyan része a betűsorozatnak az elejéről nézve, amelyben több a \(\displaystyle V\), mint a \(\displaystyle H\) betű. Az első betű alapján esetvizsgálatot végzünk.

1. eset. Az első betű \(\displaystyle V\), ekkor a maradék \(\displaystyle 6\) betű tetszőleges sorrendben következhet, így \(\displaystyle \frac{6!}{2! \cdot 4!}=15\) lehetőség van ebben az esetben.

2. eset. a) Ha az első betű \(\displaystyle H\), akkor utána következhet két \(\displaystyle V\), és ekkor a maradék \(\displaystyle 4\) (egy \(\displaystyle V\) és három \(\displaystyle H\)) betűt \(\displaystyle 4\)-féle sorrendben írhatjuk le.

b) Ha az eleje \(\displaystyle HVH\), akkor muszáj \(\displaystyle VV\)-vel folytatni, így ez \(\displaystyle 1\)-féleképpen lehetséges.

c) Ha pedig az eleje \(\displaystyle HH\), akkor utána mindenképpen a három \(\displaystyle V\) következik, így ez is \(\displaystyle 1\)-féleképpen alakulhat ki.

Több eset nincs, így összesen \(\displaystyle 15+4+1+1=21\)-féleképpen alakulhatott ki a végeredmény.

2. megoldás Írjuk le a \(\displaystyle H-V\) betűsorozatot az előző megoldás szerint, utána komplementer módszerrel dolgozunk. Összesen \(\displaystyle 7\) betű van, ezért \(\displaystyle \frac{7!}{3! \cdot 4!}=35\)-féleképpen permutálhatjuk őket, azaz a végeredmény \(\displaystyle 35\)-féleképpen alakulhatott ki. Ezek közül azokat fogjuk megszámolni, amelyek nem jók, tehát amelyekben soha nem vezettek a vendégek. Az első három betű alapján esetvizsgálatot végzünk.

1. eset. Ha az eleje \(\displaystyle HHH\), akkor bárhogyan fejezzük be, nem lesz vendégvezetés, ez \(\displaystyle 4\) lehetőséget jelent.

2. eset. Ha az eleje \(\displaystyle HHV\), akkor a maradék két-két betűt \(\displaystyle \frac{4!}{2! \cdot 2!}=6\)-féleképpen írhatjuk le. Ezek közül egyetlen esetben volt vendégvezetés \(\displaystyle (HHVVVHH)\), így \(\displaystyle 6-1=5\) lehetőséget kapunk.

3. eset. Ha az eleje \(\displaystyle HVH\), akkor az előző esethez hasonlóan \(\displaystyle 6\)-féleképpen fejezhetjük be a sort. Ezek közül csupán egy esetben volt vendégvezetés \(\displaystyle (HVHVVHH)\), így \(\displaystyle 6-1=5\) lehetőséget kapunk.

Ha a fentiektől eltérően rendezzük el az első \(\displaystyle 3\) betűt, akkor mindig lesz olyan rész az elején, amelyben több \(\displaystyle V\) betű van, mint \(\displaystyle H\), ezért több eset nincs.

Azt kaptuk, hogy \(\displaystyle 4+5+5=14\) olyan eset van, amikor nem vezettek a vendégek, így \(\displaystyle 35-14=21\) esetben vezetett a mérkőzésen a vendégcsapat.

3. megoldás Írjuk fel gólonként a lehetséges állásokat egy táblázatba. A meccs állásai úgy alakulnak ki, hogy elindulva a 0:0 mezőről jobbra lépünk (a hazai csapat lő gólt), vagy lefelé lépünk (a vendégcsapat lő gólt). Ha a vendégcsapat vezetett valamikor, akkor ez lehetett 0:1, 0:2, 0:3, 1:2, 1:3, 2:3, ezek a szürkével jelölt állások. Csak olyan állássorozaton (útvonalon) keresztül juthatunk el a 0:0-ból a 4:3-hoz, ami átmegy (legalább) egy szürkével jelölt álláson.

A lehetséges mérkőzésállások sorozatának száma megegyezik a szürke mezőt érintő útvonalak számával.

A 0:2, 0:3, 1:3 állások most nem számítanak, mert ha ezek valamelyikébe eljutunk, akkor később is lesz olyan állás, amiben a vendégcsapat vezet.

A szokásos (Pascal-háromszöges) kitöltéssel:

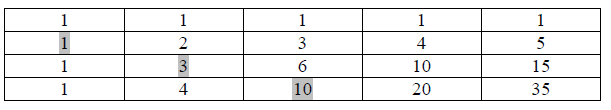
10-féleképpen juthatunk el a 2:3 álláshoz, de utána bármelyiket is csak 1 úton folytathatjuk, így ez \(\displaystyle 10\cdot1=10\) lehetőség.

3-féleképpen juthatunk el az 1:2 álláshoz, és utána 2-féleképpen fejezhetjük be az utunkat, hogy a 2:3 állást már ne érintsük (jobbra-jobbra-jobbra-le, jobbra-jobbra-le-jobbra), így ebben az esetben \(\displaystyle 3\cdot2=6\) lehetőség van.

1-féleképpen juthatunk a 0:1 állásba és innen jobbra-jobbra kell mennünk (hogy ne jussunk a 1:2 állásba, majd innen 5 lehetőségünk van továbbhaladni, hogy ne érintsük a 2:3 állást, így ez még \(\displaystyle 1\cdot5=5\) eset.

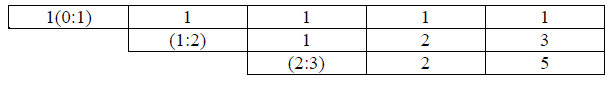
Összesen tehát \(\displaystyle 10+6+5=21\)-féleképpen alakulhatott ki a végeredmény.

Statisztika:

63 dolgozat érkezett.
5 pontot kapott:	Chen Peidong, Farkas Simon, Gáti Benjamin, Juhász Zsombor, Kámán-Gausz Péter, Máté Kristóf, Németh Ábel, Olajos Anna, Ördög Dominik, Pázmándi Renáta , Piller Zsófia, Szabó Máté, Szalóki Árpád, Tamás Attila Gábor, Tóth Luca, Válek Péter, Viczián Adél.
4 pontot kapott:	Csáki Anikó, Csikós Annamária, Pintér Lilianna.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	5 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	26 dolgozat.

A KöMaL 2024. márciusi matematika feladatai