A K. 805. feladat (2024. március)

K. 805. Rajzoljunk egy kis szabályos háromszöget, majd a következő ábrán ezt a háromszöget rakjuk körbe ugyanilyen kis háromszögekkel egy rétegben úgy, hogy egy nagyobb szabályos háromszöget kapjunk, majd ezt a második háromszöget is rakjuk körbe kis szabályos háromszögekkel úgy, hogy egy nagyobb szabályos háromszöget kapjunk, és így tovább.

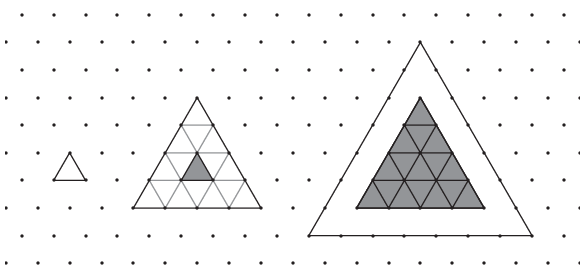
\(\displaystyle a)\) Hány kis háromszögből áll a huszadik ilyen háromszög?

\(\displaystyle b)\) Hány kis háromszögből áll az \(\displaystyle n\)-edik ilyen háromszög?

(5 pont)

A beküldési határidő 2024. április 10-én LEJÁRT.

Megoldás. A háromszögek oldalhossza minden lépésben \(\displaystyle 1+2=3\) egységgel nő (lásd az ábrát).

\(\displaystyle a)\) A 20. háromszög oldalának hossza így \(\displaystyle 1+19\cdot3=58\). Az alsó sorban \(\displaystyle 58+57=115\) kis háromszög van. A második sorban \(\displaystyle 57+56=113\), és így tovább.

\(\displaystyle b)\) Az \(\displaystyle n\)-edik háromszög oldalának hossza az a) feladat megállapítása alapján \(\displaystyle 1+(n-1)\cdot3=3n-2\). Az alsó sorban \(\displaystyle 3n-2+3n-3=6n-5\) kis háromszög van. A második sorban \(\displaystyle 3n-3+3n-4=6n-7\), és így tovább.

A kis háromszögek száma: \(\displaystyle (6n-5)+(6n-7)+(6n-9)+\dots+5+3+1\), ami egy (\(\displaystyle 3n-2\))-tagú összeg, így az eredmény \(\displaystyle =(6n-4)\cdot(3n-2):2=(3n-2)^2\).

Statisztika:

64 dolgozat érkezett.
5 pontot kapott:	Juhász Zsombor, Olajos Anna, Tóth Luca.
4 pontot kapott:	Chen Peidong, Fülöp Magdaléna, Gaál Gergely, Gyerkó Anna, Hajnal Ákos Huba, Ivák László, Németh Ábel, Pázmándi Renáta , Piller Zsófia, Sipos Levente, Szabó Medárd, Szalóki Árpád, Timár Vince , Viczián Adél.
3 pontot kapott:	16 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	3 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	24 dolgozat.

A KöMaL 2024. márciusi matematika feladatai