Problem K. 810. (April 2024)

K. 810. Trapezoid \(\displaystyle ABCD\) has the following properties: \(\displaystyle AB\parallel CD\), \(\displaystyle AB=3CD\) and \(\displaystyle CD=DA\). Find the angles of the trapezoid knowing that \(\displaystyle \angle CDA=120^{\circ}\).

German competition problem

(5 pont)

Deadline expired on May 10, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás.

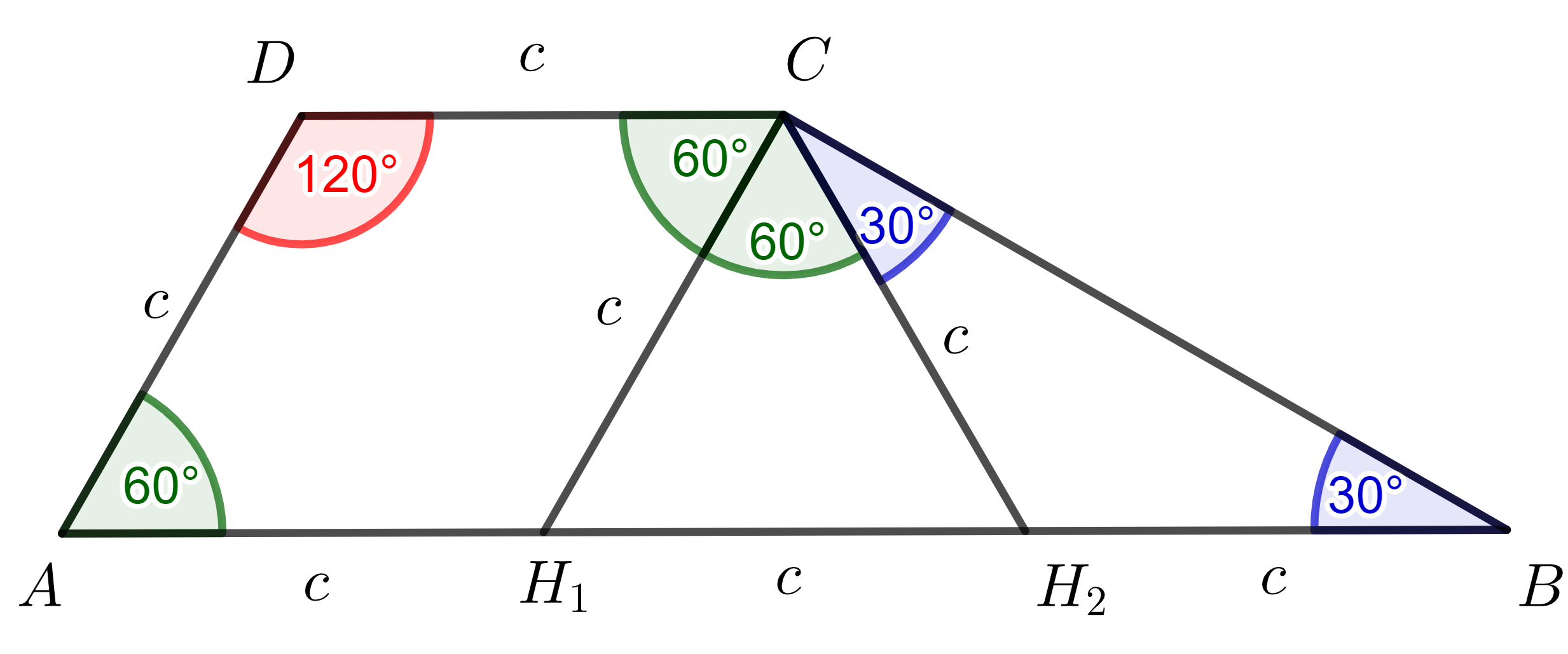
Az \(\displaystyle ABCD\) trapéz, tehát \(\displaystyle CDA \sphericalangle + DAB\sphericalangle=180^{\circ}\). Tudjuk, hogy a \(\displaystyle CDA\sphericalangle=120^{\circ}\), ezért a \(\displaystyle DAB\sphericalangle=60^{\circ}\). Jelölje \(\displaystyle H_1\) és \(\displaystyle H_2\) az \(\displaystyle AB\) oldal harmadolópontjait, továbbá jelöljük \(\displaystyle c\)-vel a \(\displaystyle CD=DA\) szakasz hosszát. Ekkor tehát \(\displaystyle CD=DA=AH_1=H_1H_2=H_2B=c\). Mivel \(\displaystyle CD=AH_1\) és \(\displaystyle DC \parallel AH_1\), az \(\displaystyle AH_1CD\) négyszög parallelogramma, hiszen két szemközti oldala párhuzamos és egyenlő. Így \(\displaystyle DCH_1\sphericalangle=60^{\circ}\), továbbá \(\displaystyle AH_1C\sphericalangle=120^{\circ}\), valamint \(\displaystyle CH_1=c\). Ekkor a \(\displaystyle CH_1H_2 \triangle\) szabályos, ugyanis egyenlő szárú, és a két szár által bezárt szöge \(\displaystyle 60^{\circ}\). Ebből következően \(\displaystyle CH_2=c\), tehát a \(\displaystyle CH_2B\triangle\) is egyenlő szárú, szárszöge pedig \(\displaystyle 120^{\circ}\). Ennek a háromszögnek tehát az alapon fekvő szögei \(\displaystyle H_2BC\sphericalangle=BCH_2\sphericalangle=30^{\circ}\). Összefoglalva tehát az \(\displaystyle ABCD\) trapéz kérdéses szögei :

\(\displaystyle DAB\sphericalangle=60^{\circ}, \hspace{0.5 cm} H_2BC\sphericalangle=30^{\circ}, \hspace{0.5cm}BCD\sphericalangle=150^{\circ}.\)

Statistics:

89 students sent a solution.
5 points:	Araguas Mátyás, Bihi Boglárka, Bubálik Nóra, Chen Peidong, Csáki Anikó, Dömők Bernadett, Farkas Simon, Feith Benedek, Fülöp Magdaléna, Gáti Benjamin, Gyerkó Anna, Hajnal Ákos Huba, Ivák László, Juhász Zsombor, Kiss Domonkos László, Kóródy Vera, Kőhidi Kata, Máté Kristóf, Mondovics Gábor , Németh Ábel, Olajos Anna, Pázmándi Renáta , Péterfia Kamilla, Pintér Lilianna, Pivárcsik Márk, Sajó Marcell 16, Sipos Dániel Sándor, Sipos Levente, Szabó Máté, Szalóki Árpád, Szedmák Szabrina, Tamás Attila Gábor, Timár Vince , Tóth Luca, Válek Péter, Viczián Adél.
4 points:	Fitori Csanád, Gaál Gergely, Gárdonyi Zsolt, Mezei Kamilla , Paksy-Szabó Győző , Roszik Szabolcs, Tóth Bálint Levente, Yan Zhebeier.
3 points:	7 students.
2 points:	2 students.
1 point:	2 students.
Not shown because of missing birth date or parental permission:	34 solutions.

Problems in Mathematics of KöMaL, April 2024