A K. 815. feladat (2024. május)

K. 815. Az $\displaystyle ABC$ derékszögű háromszög $\displaystyle BC$ befogóján úgy vettük fel a $\displaystyle D$ pontot, hogy $\displaystyle BC=4BD$, az $\displaystyle AC$ befogón felvett $\displaystyle E$ pontra pedig $\displaystyle AC=8CE$ teljesül.
Határozzuk meg az $\displaystyle AB$ átfogó hosszát, ha tudjuk, hogy $\displaystyle AD=164$ és $\displaystyle BE=52$.

vietnámi feladat

(5 pont)

A beküldési határidő 2024. június 10-én LEJÁRT.

Megoldás.

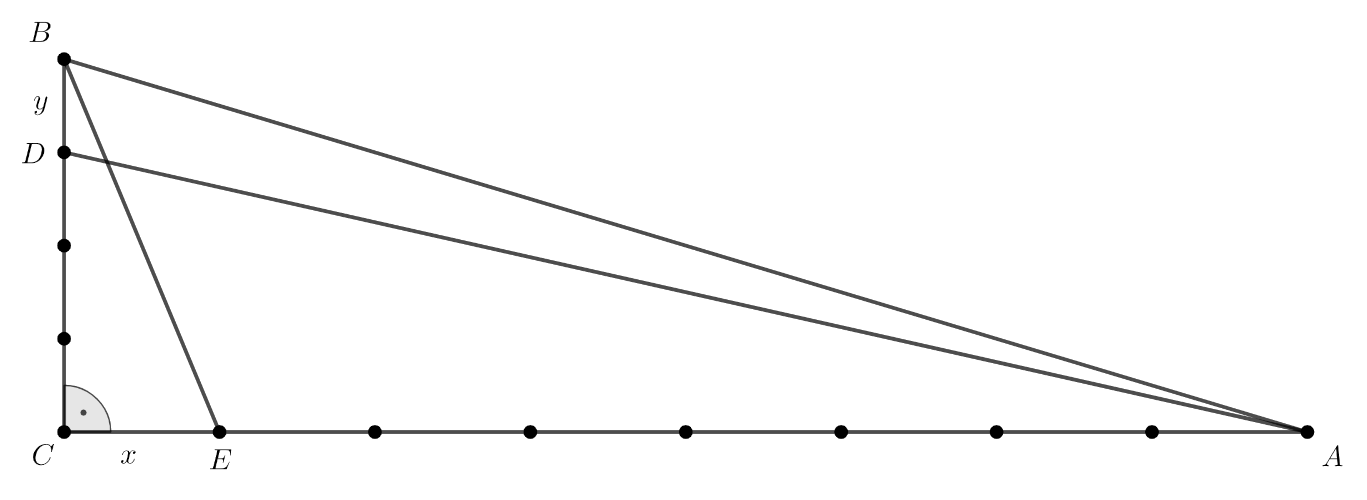
Legyen $\displaystyle CE=x$, és $\displaystyle BD=y$. A $\displaystyle CEB$ és a $\displaystyle CAD$ háromszög derékszögű, így oldalaikra felírható a Pitagorasz-tétel:

$\displaystyle x^2+(4y)^2=52^2,$

$\displaystyle (8x)^2+(3y)^2=164^2.$

Oldjuk meg a fenti egyenletrendszert, ahol $\displaystyle x$ és $\displaystyle y$ pozitív számokat jelölnek. Először bontsuk ki a zárójeleket:

$\displaystyle x^2+16y^2=2704,$

$\displaystyle 64x^2+9y^2=26896;$

majd szorozzuk meg az első egyenletet $\displaystyle 64$-gyel:

$\displaystyle 64x^2+1024y^2=173056,$

$\displaystyle 64x^2+9y^2=26896,$

és vonjuk ki az így keletkezett első egyenletből a másodikat, kiküszöbölve ezzel az $\displaystyle x^2$-et. Ezzel a lépéssel nem veszítünk gyököt.

$\displaystyle 1015y^2=146160.$

Egy osztás után adódik $\displaystyle y^2$ értéke, valamint $\displaystyle y$-é is, hiszen $\displaystyle y$ csak pozitív lehet:

$\displaystyle y^2=144,$

$\displaystyle y=12.$

Ebből következően $\displaystyle x^2$-et is ki tudjuk számolni a legelső egyenletünk segítségével:

$\displaystyle x^2+(4\cdot12)^2=2704,$

$\displaystyle x^2=2704-2304=400,$

$\displaystyle x=20.$

Ebből következően $\displaystyle CA=160$, $\displaystyle CB=48$. Az $\displaystyle ABC$ háromszögre felírva a Pitagorasz-tételt, azt kapjuk, hogy

$\displaystyle 160^2+48^2=27904=AB^2=2^8\cdot 109.$

Így az átfogó keresett hossza:

$\displaystyle BC=16\sqrt{109}\approx 167,0449.$

Statisztika:

50 dolgozat érkezett.
5 pontot kapott:	Bubálik Nóra, Chen Peidong, Csáki Anikó, Dömők Bernadett, Farkas Simon, Fülöp Magdaléna, Gaál Gergely, Gáti Benjamin, Hajnal Ákos Huba, Juhász Zsombor, Kámán-Gausz Péter, Kóródy Vera, Máté Kristóf, Németh Ábel, Olajos Anna, Pázmándi Renáta , Roszik Szabolcs, Sipos Dániel Sándor, Szabó Máté, Szalóki Árpád, Szedmák Szabrina, Tamás Attila Gábor, Tóth Luca, Válek Péter, Viczián Adél.
4 pontot kapott:	Feith Benedek, Kovács 007 Benedek, Módis Marcell, Ördög Dominik, Papp Emese Petra, Pintér Lilianna, Sipos Levente, Szabó Medárd, Timár Vince .
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	16 dolgozat.

A KöMaL 2024. májusi matematika feladatai