A K. 836. feladat (2024. december)

K. 836. Az \(\displaystyle ABC\) derékszögű háromszög egységnyi hosszúságú \(\displaystyle AB\) befogójának \(\displaystyle B\)-n túli meghosszabbításán felvettük a \(\displaystyle D\) pontot úgy, hogy \(\displaystyle BD=\dfrac{AC}{2}\) teljesüljön. Az \(\displaystyle AC\) befogó felezőpontja \(\displaystyle E\). Az \(\displaystyle AED\) és \(\displaystyle ABC\) háromszögek területének aránya \(\displaystyle 2:3\). Határozzuk meg \(\displaystyle BD\) hosszát.

(5 pont)

A beküldési határidő 2025. január 10-én LEJÁRT.

Megoldás. Tekintsük az ábrát. Jelölje \(\displaystyle BD\) hosszát \(\displaystyle x\).

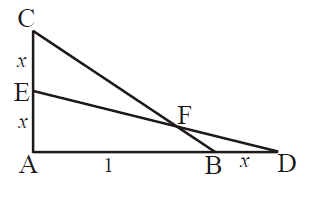
A két háromszög területének aránya:

\(\displaystyle \frac{T_{EAD}}{T_{ABC}}=\frac{0,5\cdot(1+x)\cdot x}{0,5\cdot1\cdot2x}=\frac{1+x}{2}=\frac23\), innen \(\displaystyle x=\frac13\). Tehát a \(\displaystyle BD\) szakasz hossza \(\displaystyle \frac13\) egységnyi.

Statisztika:

A K. 836. feladat értékelése még nem fejeződött be.

A KöMaL 2024. decemberi matematika feladatai