A K. 845. feladat (2025. február)

K. 845. Az alábbi \(\displaystyle 3\times3\)-as táblázatba írjuk be az \(\displaystyle 1\), \(\displaystyle 2\), \(\displaystyle 3\), \(\displaystyle 4\), \(\displaystyle 5\), \(\displaystyle 6\), \(\displaystyle 7\), \(\displaystyle 9\), \(\displaystyle 10\) számokat úgy, hogy bármelyik két oldalszomszédos mezőn lévő szám összege prímszám legyen. Hány megoldása van a feladatnak? (Két megoldás különböző, ha van olyan szám, amelynek mások a szomszédai az egyik, illetve a másik elrendezésben.)

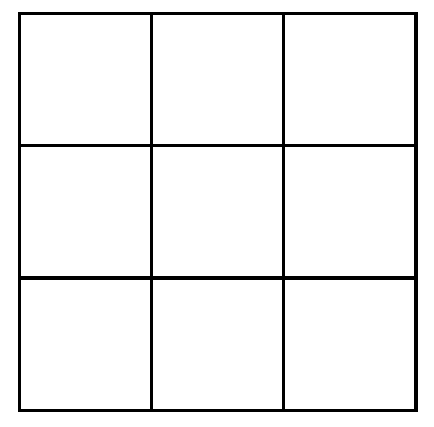
(5 pont)

A beküldési határidő 2025. március 10-én LEJÁRT.

Megoldás. Két egész szám összege csak úgy lehet 2-nél nagyobb prímszám, ha az egyik páros, a másik páratlan. (A feltételek miatt a 2 nem lehet összeg.) Mivel a megadott 9 szám között 5 páratlan és négy páros van, így csakis olyan elrendezés lehetséges, melyben a középső, illetve a sarokmezőkre páratlan szám kerül, az oldalközepekre pedig páros szám.

űA 9 nem kerülhet középre, mert akkor a 6 mellé kerül és az összegük 15, ami nem prím.

A 7 nem kerülhet középre, mert akkor a 2 mellé kerül és az összegük 9, ami nem prím.

Az 5 nem kerülhet középre, mert akkor a 10 mellé kerül és az összegük 15, ami nem prím.

A 3 nem kerülhet középre, mert akkor a 6 mellé kerül és az összegük 9, ami nem prím.

Az 1 kerülhet középre, mert \(\displaystyle 2+1=3\), \(\displaystyle 4+1=5\), \(\displaystyle 6+1=7\), \(\displaystyle 10+1=11\) prímszámok.

Összesen tehát négy megoldása van a feladatnak.

Legyen a 2 felül középen. Vele szemben a 4, a 6 vagy a 10 lehet és ekkor a másik két páros szám elhelyezése már adott (a sorrendjük nem számít, mert ugyanannak az elrendezésnek a tükörképét kapnánk a másik sorrendben.)

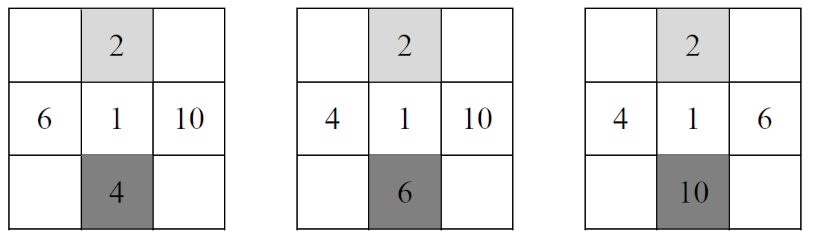
Az első táblázatban a 3 a jobb felső vagy a jobb alsó sarokba kerülhet, az 5 csak a bal felső sarokba, a 7 a két alsó sarokmezőbe, a 9 a jobb felső vagy a jobb alsó mezőbe mehet.

Ezek alapján az első esetben két megfelelő elrendezés van:

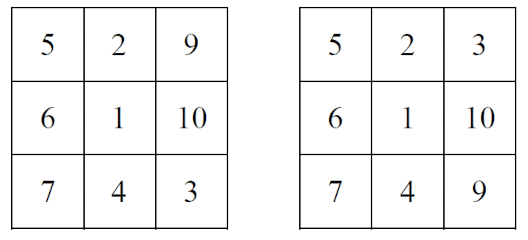
A második táblázatban az 5-öt nem lehet elhelyezni, mert vagy a 4-gyel ad 9-es összeget, vagy a 10-zel 15-öt, így itt nincs megoldás.

A harmadik táblázatban a 3 a bal felső vagy a bal alsó mezőbe mehet, az 5 csak a jobb felső mezőbe, a 7 a két alsó sarokmezőbe, a 9 a bal felső vagy a bal alsó mezőbe mehet.

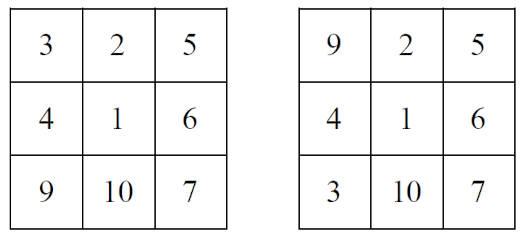
Statisztika:

A K. 845. feladat értékelése még nem fejeződött be.

A KöMaL 2025. februári matematika feladatai