 |
A K. 849. feladat (2025. március) |
K. 849. Legalább hány gyufát kell elvenni ahhoz, hogy az ábrán semmilyen méretű négyzet ne maradjon?
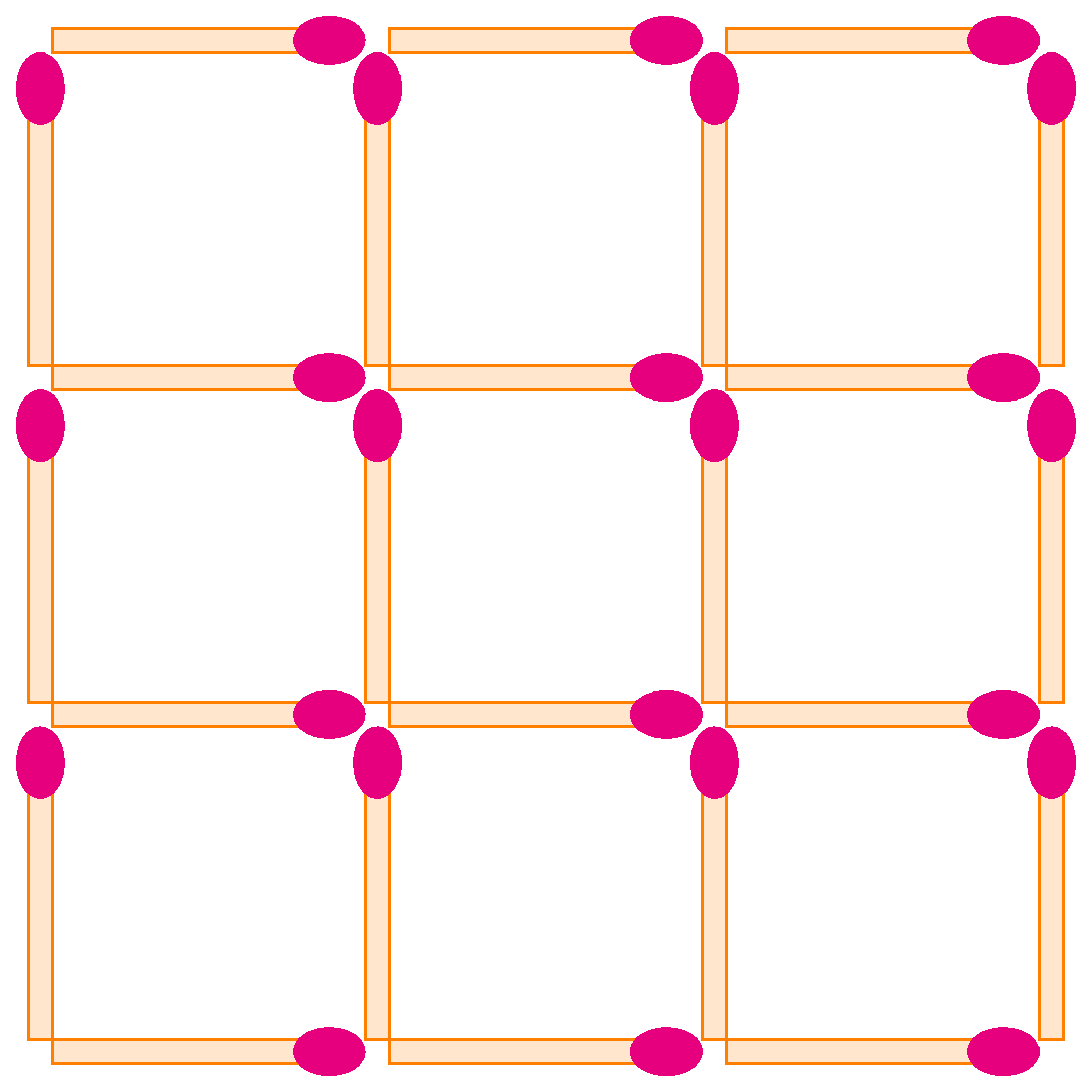
(5 pont)
A beküldési határidő 2025. április 10-én LEJÁRT.
Megoldás. Ha csak a kis négyzeteket szeretnénk megszüntetni, akkor ehhez legalább öt gyufa elvétele szükséges, mert egy gyufa legfeljebb két kis négyzethez tartozhat.
A négy darab 2×2-es négyzet megszüntetéséhez két gyufa elvétele elegendő, mert a gyufasorok, illetve gyufaoszlopok közepén lévő gyufák két-két ilyen négyzethez is tartoznak.
A legnagyobb négyzet megszüntetéséhez el kell venni egy gyufát az ábra külső 12 gyufája közül.
Öt gyufa elvétele nem elég. Egy biztosan a külső gyufák közül való (a nagy négyzet miatt). A kerületről elvett gyufa által megszűnt kis négyzeten kívül 8 darab kis négyzetet kell páronként egy-egy gyufa elvételével megszüntetni.
Ha az oldal egyik középső gyufáját vesszük el, akkor nem is lehet párosával megszüntetni a megmaradó 8 kis négyzetet (Lásd ábra!).
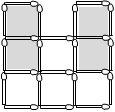
Ha az oldal egyik szélső gyufáját vesszük el, akkor végignézve a lehetőségeket mindegyik esetben marad egy-egy 2×2-es négyzet. (Lásd ábra.)

Hat gyufa elvételével megoldható. Pl:

Statisztika:
97 dolgozat érkezett. 5 pontot kapott: Csík Zoltán Richárd, Holló Barnabás, Izsa Ferenc Gergő, Laczó Zoltán, Lovas Márk, Medgyesi András, Nagy Alexander, Patócs 420 Péter, Rózsa Péter. 4 pontot kapott: Bloemsma Péter Sándor, Kudomrák Lili Anna , Mátyás Levente, Molnár Levente. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 30 versenyző. 0 pontot kapott: 22 versenyző. Nem versenyszerű: 5 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 9 dolgozat.
A KöMaL 2025. márciusi matematika feladatai
|
|

