A K. 851. feladat (2025. március)

K. 851. Daraboljuk fel az ábrán látható öt egybevágó négyzetből álló alakzatot három részre két vágással úgy, hogy ha a darabokat megfelelően összeillesztjük, akkor egy olyan téglalapot kapjunk, amelynek az egyik oldala kétszer olyan hosszú, mint a másik.

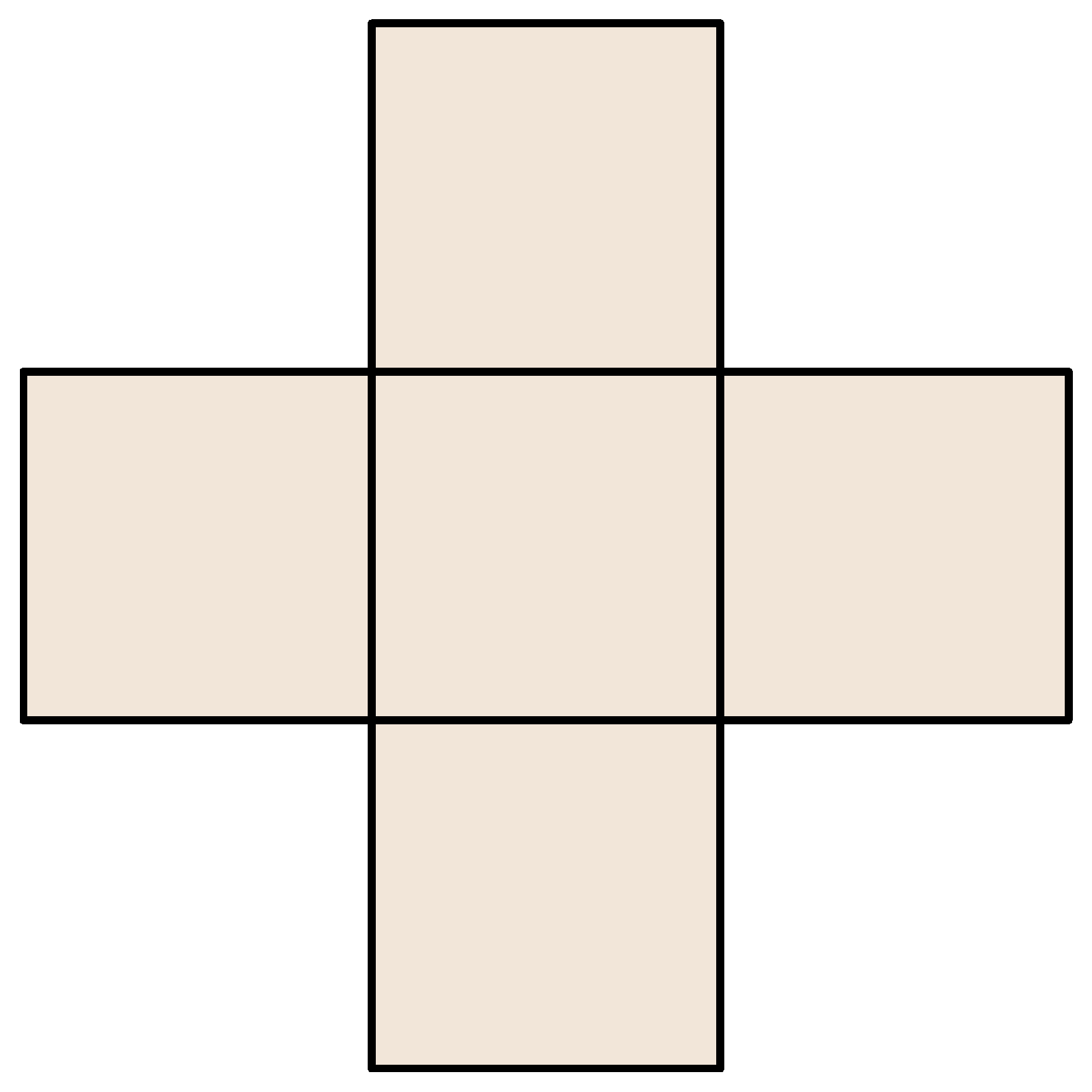
(5 pont)

A beküldési határidő 2025. április 10-én LEJÁRT.

Megoldás. Ha a négyzet oldala 1 egység, akkor az alakzat, illetve a téglalap területe 5 egység. Legyen a téglalap egyik oldala $\displaystyle b$, akkor a másik oldala $\displaystyle 2b$, így $\displaystyle 2b^2=5$. azaz $\displaystyle b=\sqrt{2,5}$, a hosszabbik oldal pedig $\displaystyle 2b=2\sqrt{2,5}=\sqrt{10}$. Első lépésként húzzuk be pl. a vízszintes $\displaystyle 3\times1$-es téglalap átlóját, mely a Pitagorasz-tétel miatt $\displaystyle \sqrt{10}$ hosszúságú, majd megrajzolva a megfelelő erre merőleges $\displaystyle b$ oldalt gyorsan adódik a felbontás.

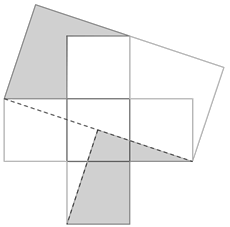
Statisztika:

56 dolgozat érkezett.
5 pontot kapott:	Bloemsma Péter Sándor, Chen Zhibo, Csík Zoltán Richárd, Fórján Bernát, Győrffy Csanád, Hajdu Vince, Havasi Máté Pál, Holló Barnabás, Izsa Ferenc Gergő, Kása Richárd Zsolt, Kovács 444 Kamilla, Kovács Domonkos, Kudomrák Lili Anna , Kun Milán, Laczó Zoltán, Lovas Márk, Majer Veronika, Máté Zsófia, Mátyás Levente, Medgyesi András, Miskolczi Dóra, Molnár Levente, Nagy Alexander, Patócs 420 Péter, Péter Tamás, Radošická Emma, Rózsa Péter, Silye Zalán, Szabó Anita, Szabó Flóra, Szighardt Anna, Zsilák Márk Péter.
4 pontot kapott:	Robb Horkay Jázmin, Szabó Balázs.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	8 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	5 dolgozat.

A KöMaL 2025. márciusi matematika feladatai