Az M. 382. feladat (2018. december)

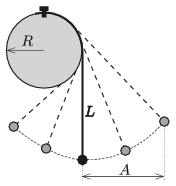
M. 382. Egy vékony, hajlékony, nyújthatatlannak tekinthető fonál egyik végét egy $\displaystyle R$ sugarú, vízszintes tengelyű, rögzített henger ,,tetejéhez'' erősítjük, a másik végére pedig egy kis méretű testet akasztunk. Egyensúlyi állapotban a fonál függőleges darabja $\displaystyle L=3R$ hosszúságú. A testet az ábrán látható módon kitérítjük, majd magára hagyjuk. A test mozgásának periódusideje – viszonylag nagy kezdeti kitérésnél – függ az $\displaystyle A$ ,,amplitúdótól''. Mérjük meg néhány különböző $\displaystyle A$ esetén, hogy hány százalékkal tér el ezen inga (ún. evolvens­inga) $\displaystyle T(A)$ lengésideje az $\displaystyle L$ hosszúságú fonálinga $\displaystyle T_0=2\pi\sqrt{{L}/{g}}$ lengésidejétől!

Christiaan Huygens (1629–1695) nyomán

(6 pont)

A beküldési határidő 2019. január 10-én LEJÁRT.

Statisztika:

11 dolgozat érkezett.
6 pontot kapott:	Kondákor Márk, Kozák 023 Áron, Olosz Adél, Pácsonyi Péter.
5 pontot kapott:	Fülöp Sámuel Sihombing, Morvai Orsolya, Varga 235 Áron.
4 pontot kapott:	2 versenyző.
3 pontot kapott:	2 versenyző.

A KöMaL 2018. decemberi fizika feladatai