A P. 4241. feladat (2010. március)

P. 4241. Ideális gáz az ábrán látható körfolyamatot végzi.

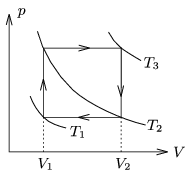
\(\displaystyle a)\) Milyen kapcsolat van \(\displaystyle T_{1}\), \(\displaystyle T_{2}\) és \(\displaystyle T_{3}\) között?

\(\displaystyle b)\) Fejezzük ki a körfolyamatot végző hőerőgép hatásfokát \(\displaystyle x=\frac{V_{2}}{V_{1}}\) és \(\displaystyle \kappa=\frac{c_{p}}{c_{V}}\) segítségével!

\(\displaystyle c)\) Levegő esetén milyen határok között változhat ez a hatásfok?

Közli: Légrádi Imre, Sopron

(4 pont)

A beküldési határidő 2010. április 12-én LEJÁRT.

Megoldás. \(\displaystyle a)\) \(\displaystyle T_2=\sqrt{T_1T_3},\)

\(\displaystyle b)\) \(\displaystyle \eta=\frac{(\kappa-1)(x-1)}{1+\kappa x},\)

\(\displaystyle c)\) \(\displaystyle 0<\eta<2/7\).

Statisztika:

53 dolgozat érkezett.
4 pontot kapott:	Balogh Gábor, Batki Bálint, Benyó Krisztián, Dénes Benjámin, Filep Gábor, Fonai Dániel, Janosov Milán, Kaposvári István, Nagy 111 Miklós, Pataki Bálint Ármin, Patartics Bálint, Varju 105 Tamás, Vuchetich Bálint, Zsámboki Richárd.
3 pontot kapott:	Béres Bertold, Bolgár Dániel, Czigány Máté Gábor, Farkas Martin, Fülöp András, Hartstein Máté, Hegedűs Csaba, Jéhn Zoltán, Kovács Attila, Kulcsár Flóra, Kungl Ákos Ferenc, Mayer Martin János, Molnár Alexandra, Pázmán Koppány, Pető János, Tamási Mátyás.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	6 versenyző.
Nem versenyszerű:	5 dolgozat.

A KöMaL 2010. márciusi fizika feladatai