A P. 4247. feladat (2010. április)

P. 4247. Az ábra szerinti rögzített, \(\displaystyle \alpha=30^\circ\)-os hajlásszögű, súrlódásmentes lejtő egy adott pontja feletti \(\displaystyle h\) magasságból \(\displaystyle t_{1}\) idő alatt esik a lejtőre egy kisméretű test. A teljesen rugalmatlan ütközés után \(\displaystyle t_{2}\) idő alatt tesz meg ugyanekkora \(\displaystyle s=h\) távolságot a lejtőn. Mekkora a \(\displaystyle t_{1}/t_{2}\) arány?

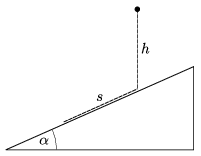
Közli: Holics László, Budapest

(4 pont)

A beküldési határidő 2010. május 10-én LEJÁRT.

Megoldás. \(\displaystyle t_1/t_2=(\sqrt{3}+1)/2\approx1,\!37\).

Statisztika:

109 dolgozat érkezett.
4 pontot kapott:	Balogh Gábor, Barta Szilveszter Marcell, Batki Bálint, Béres Bertold, Béres Orsolya Katalin, Bodosi Eszter, Fekete Károly, Filep Gábor, Fonai Dániel, Fülep Andrea , Galzó Ákos Ferenc, Győrfi 946 Mónika, Hartstein Máté, Janosov Milán, Kánvási Dániel, Kaposvári István, Kerti Dávid, Kollarics Sándor, Kovács 616 Philip, Kungl Ákos Ferenc, Laczkó Zoltán Balázs, Lájer Márton, Mayer Martin János, Miskó Gergely, Neumer Tamás, Para Attila, Pázmán Koppány, Rácz Viktor, Réti Dávid, Sápi András, Szabó Bence, Szélig Áron, Szentgyörgyi 994 Rita, Takács 737 Gábor, Virág Máté, Wirnhardt Bálint.
3 pontot kapott:	Koncz Gabriella.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	56 versenyző.
0 pontot kapott:	11 versenyző.

A KöMaL 2010. áprilisi fizika feladatai