 |
A P. 4271. feladat (2010. szeptember) |
P. 4271. Homogén, függőlegesen lefelé mutató, \(\displaystyle B=0{,}5~\)T indukciójú mágneses erőtérben két párhuzamos, vízszintes síkú, egymástól \(\displaystyle \ell=10\) cm-re lévő vezető sínt \(\displaystyle U_{0}=12~\)V feszültségű akkumulátorral kötünk össze. A sínekre, rájuk merőlegesen, \(\displaystyle m=50~\)g tömegű, \(\displaystyle R=2~\Omega\) ellenállású fémrudat fektetünk. A fémrúd és a sín között \(\displaystyle \mu=0{,}3\) a súrlódási együttható.
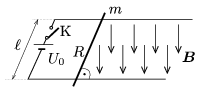
\(\displaystyle a)\) Mekkora gyorsulással indul el a fémrúd a K kapcsoló zárása után?
\(\displaystyle b)\) Mekkora sebességre gyorsulhatna fel a rúd, ha a sín igen hosszú lenne?
\(\displaystyle c)\) Becsüljük meg minél pontosabban, hogy mennyi idő alatt és mekkora úton nő a rúd sebessége 4,0 \(\displaystyle \frac{\rm m}{\rm s}\)-ról 4,1 \(\displaystyle \frac{\rm m}{\rm s}\)-ra!
Wigner Jenő verseny, Békéscsaba
(5 pont)
A beküldési határidő 2010. október 11-én LEJÁRT.
Megoldás. \(\displaystyle a)\) A kezdeti gyorsulás \(\displaystyle 3~\textrm{m/s}^2\).
\(\displaystyle b)\) A rúd végsebessége 120 m/s lehet.
\(\displaystyle c)\) 34 ms alatt 14 cm-es úton gyorsul fel a rúd 4,0 m/s-ról 4,1 m/s sebességre.
Statisztika:
76 dolgozat érkezett. 5 pontot kapott: Ayhan Dániel, Bánhidi Dávid, Barta Szilveszter Marcell, Batki Bálint, Béres Bertold, Czigány Máté Gábor, Dávid Péter, Filep Gábor, Gál Szabolcs, Gargauly Gergő János, Herczeg Ferenc, Jéhn Zoltán, Jenei Márk, Kóbor Attila, Kovács 444 Áron, Köpenczei Gergő, Laczkó Zoltán Balázs, Lőrincz Dóra, Maknics András, Nagy 111 Miklós, Nagy Dániel Bálint, Nagy Lajos, Németh Gergely, Pázmán Koppány, Prok Tamás, Schwarcz Gergő, Seress Dániel, Szabó 928 Attila, Szélig Áron, Szemes Gábor Bence, Szikszai Lőrinc, Szöllősi Márton, Tamási Mátyás, Varga 515 Balázs, Vargha Sára, Várnai Péter, Vuchetich Bálint. 4 pontot kapott: 19 versenyző. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2010. szeptemberi fizika feladatai