 |
A P. 4290. feladat (2010. november) |
P. 4290. Egy utca felett vékony, erős, hajlékony drótkötelet (acélsodronyt) feszítenek ki nagy erővel, vízszintesen. Egy kötéltáncos lassan végigmegy a kötélen. Amikor a negyedrészhez (\(\displaystyle N\) ponthoz) ér, a kötél harmadolópontja (\(\displaystyle H\)) 10 cm-rel van mélyebben az eredeti helyzeténél.
Mennyi lesz az \(\displaystyle N\) pont lesüllyedése, amikor a kötéltáncos a \(\displaystyle H\) ponthoz ér? (A kötél súlya elhanyagolható, továbbá a kötél lehajlása nagyon kicsi a kötél hosszához képest, és a kötélben ható feszítőerőt jó közelítéssel állandónak tekinthetjük.)
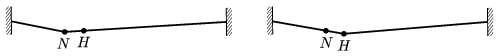
Közli: Gnädig Péter, Vácduka
(5 pont)
A beküldési határidő 2010. december 10-én LEJÁRT.
Megoldás. Az \(\displaystyle N\) pont lesüllyedése is éppen 10 cm lesz. (Ez az érdekes szimmetriatulajdonság a kötél tetszőleges két pontjára igaz.)
Statisztika:
31 dolgozat érkezett. 5 pontot kapott: Batki Bálint, Béres Bertold, Bolgár Dániel, Dinev Georgi, Gargauly Gergő János, Juhász Péter, Laczkó Zoltán Balázs, Mázik László, Nagy Dániel Bálint, Pázmán Koppány, Szabó 928 Attila, Szélig Áron, Szikszai Lőrinc, Várnai Péter. 4 pontot kapott: Antalicz Balázs, Barta Szilveszter Marcell, Szigeti Bertalan György. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 9 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2010. novemberi fizika feladatai

