A P. 4308. feladat (2011. január)

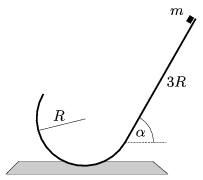
P. 4308. A vízszintessel =60^o-os szöget bezáró, 3R hosszúságú sima lejtő alsó, vízszintes élével törésmentesen csatlakozik egy R=0,5 m sugarú, félkörív keresztmetszetű hengerfelülethez. A lejtő tetejéről kezdősebesség nélkül lecsúszik egy pontszerűnek tekinthető, m=0,2 kg tömegű test.

a) Mekkora lesz a test mozgási energiája a lejtő alját követő pályájának legmagasabb pontján?

b) Hol csapódik a test a lejtőre?

(A súrlódás és a közegellenállás elhanyagolható.)

Közli: Holics László, Budapest

(5 pont)

A beküldési határidő 2011. február 10-én LEJÁRT.

Megoldás. \(\displaystyle a)\) A kis test mechanikai energiája megmarad, ezért pályájának legmagasabb pontján a mozgási energiája

\(\displaystyle E=\cos^2\alpha(3\sin\alpha-2\cos\alpha)mgR=\frac{3\sqrt{3}-2}{8}mgR\approx 0,\!39~\rm J\)

értékű lesz.

\(\displaystyle b)\) A kis test a lejtő és a hengerfelület csatlakozási vonalától

\(\displaystyle \ell=2\left(\sqrt{6\tg\alpha-4}-\tg\alpha\right)\,R=2\left( \sqrt{2(3\sqrt{3}-2)}-\sqrt{3} \right)\,R\approx 0{,}8~\rm m\)

távolságra csapódik a lejtőbe (ennek kiszámítására a legegyszerűbb mód, ha elforgatott koordinátarendszert használunk).

Statisztika:

110 dolgozat érkezett.
5 pontot kapott:	Ayhan Dániel, Barta Szilveszter Marcell, Batki Bálint, Bolgár Dániel, Csáky Pál, Fonyó Viktória, Garami Anna, Jenei Márk, Kabos Eszter, Kovács 255 Márton, Maknics András, Nagy Lajos, Papp Roland, Pataki Bálint Ármin, Sisák Mária Anna, Szabó 928 Attila, Szegedi Domonkos, Szélig Áron, Szikszai Lőrinc, Tamási Mátyás, Varga 515 Balázs, Zsámboki Richárd.
4 pontot kapott:	Antalicz Balázs, Béres Bertold, Csóka József, Dálya Gergely, Damokos József, Emri Tamás, Gargauly Gergő János, Gróf Gábor, Kalácska Dániel, Kaposvári Péter, Károlyi Áron, Kollarics Sándor, Koncz Gabriella, Kovács 737 Ármin, Kozák Ádám András, Kunsági-Máté Sándor, Lőrincz Dóra, Nagy Dániel Bálint, Németh 241 Ilona, Park Choong Eun, Schwarcz Gergő, Simon Sebestyén, Szigeti Bertalan György, Timkó Réka, Zahemszky Péter.
3 pontot kapott:	31 versenyző.
2 pontot kapott:	12 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	5 versenyző.
Nem versenyszerű:	8 dolgozat.

A KöMaL 2011. januári fizika feladatai