Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A P. 4422. feladat (2012. február)

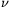P. 4422. A pion (\pi+) az elektronnál 273-szor nagyobb tömegű elemi részecske, melynek egyik lehetséges bomlási folyamatában pozitron (e+) és elektron-neutrínó (\nue) keletkezik:

\pi^+\quad \longrightarrow \quad e^+ + \nu_{\rm e}.

Legalább mekkora annak a pionnak a sebessége, amelynek bomlásában a pozitron és a neutrínó egymásra merőlegesen repülnek szét?

(A neutrínót tekintsük zérus nyugalmi tömegűnek, azaz olyan részecskének, melynek energiája és impulzusa között fennáll az E=pc összefüggés.)

Közli: Vigh Máté, Pécs

(6 pont)

A beküldési határidő 2012. március 12-én LEJÁRT.

Megoldás. \(\displaystyle v_{\pi}^{\rm min}=\frac{c}{\sqrt{2}}\approx 0{,}7\,c=2{,}1\cdot 10^8~\frac{\rm m}{\rm s}.\)

Statisztika:

21 dolgozat érkezett.
6 pontot kapott:Barta Szilveszter Marcell, Bolgár Dániel, Czipó Bence, Dinev Georgi, Garami Anna, Jenei Márk, Juhász Péter, Koncz Gabriella, Kovács 444 Áron, Laczkó Zoltán Balázs, Papp Roland, Szabó 928 Attila, Ürge László.
5 pontot kapott:Machó Bónis, Táczi István.
4 pontot kapott:3 versenyző.
3 pontot kapott:1 versenyző.
1 pontot kapott:1 versenyző.
0 pontot kapott:1 versenyző.

A KöMaL 2012. februári fizika feladatai