 |
A P. 4609. feladat (2014. február) |
P. 4609. Egy vízszintes, vékony cső mindkét vége zárt. A cső közepén egy h hosszúságú higanyszál van. A levegőoszlopok hossza mindkét térrészben  , a nyomás mindkét oldalon H magasságú higanyoszlop hidrosztatikai nyomásával egyenlő. A csövet egy függőleges tengelyű centrifugagépre helyezzük, és forgásba hozzuk.
, a nyomás mindkét oldalon H magasságú higanyoszlop hidrosztatikai nyomásával egyenlő. A csövet egy függőleges tengelyű centrifugagépre helyezzük, és forgásba hozzuk.
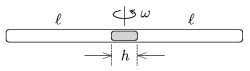
Adjuk meg a higanyszál elmozdulását az  szögsebesség függvényében, ha a hőmérséklet állandó!
szögsebesség függvényében, ha a hőmérséklet állandó!
Varga István (1952-2007) feladata
(5 pont)
A beküldési határidő 2014. március 10-én LEJÁRT.
Megoldásvázlat. Az elmozdulás \(\displaystyle x=\ell\sqrt{1-\left(\frac{\omega_\text{krit.}}{\omega}\right)^2}\), ha \(\displaystyle \omega>\omega_\text{krit.}=\sqrt{\frac{2gH}{\ell h}},\) egyébként \(\displaystyle x=0\) (tehát a higanyszál nem mozdul ki a középső helyzetéből).
Statisztika:
51 dolgozat érkezett. 5 pontot kapott: Asztalos Bogdán, Balogh Menyhért, Blum Balázs, Bugár 123 Dávid, Csathó Botond, Fehér Zsombor, Gróf Tamás, Holczer András, Horicsányi Attila, Horváth 974 Bence Attila, Iván Balázs, Janzer Barnabás, Juhász Péter, Kovács Péter Tamás, Sal Kristóf, Wiandt Péter. 4 pontot kapott: Antalicz Balázs, Berta Dénes, Dinev Georgi, Farkas Tamás, Forrai Botond, Huszár Emese, Kacz Dániel, Kaposvári Péter, Kasza Bence, Krokos Ádám László, Marosvári Kristóf, Molnár 128 Szilárd, Németh Flóra Boróka, Olosz Balázs, Öreg Botond, Pázmán Zalán, Sárvári Péter, Seress Dániel, Szántó Benedek, Szász Norbert Csaba, Szépfalvi Bálint, Varju Ákos. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2014. februári fizika feladatai

