 |
A P. 4622. feladat (2014. március) |
P. 4622. \(\displaystyle N=100\) darab egyforma galvánelemet az ábrán látható módon teleppé kapcsolunk össze. Mindegyik galvánelem üresjárati feszültsége \(\displaystyle U_0\), belső ellenállása \(\displaystyle R_{\rm b}\).
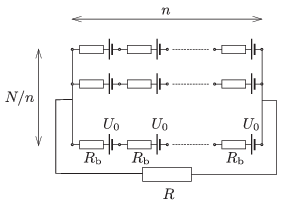
Milyen elrendezés esetén adja le ez a telep a legnagyobb teljesítményt egy külső \(\displaystyle R\) ellenálláson, ha
\(\displaystyle a)\) \(\displaystyle R=R_{\rm b};\)
\(\displaystyle b)\) \(\displaystyle R=4R_{\rm b};\)
\(\displaystyle c)\) \(\displaystyle R=5R_{\rm b}?\)
Közli: Radnai Gyula, Budapest
(5 pont)
A beküldési határidő 2014. április 10-én LEJÁRT.
Megoldásvázlat. A leadott teljesítmény: \(\displaystyle P=\left( \frac{n U_0 }{R+ \frac{n^2}{N}R_{\rm b}}\right)^2 R.\)
\(\displaystyle a)\) \(\displaystyle P_\text{max}=25\cdot\frac{U_0^2}{R_{\rm b}}\), ha \(\displaystyle n=10\).
\(\displaystyle b)\) \(\displaystyle P_\text{max}=25\cdot\frac{U_0^2}{R_{\rm b}}\), ha \(\displaystyle n=20\).
\(\displaystyle c)\) \(\displaystyle P_ {\rm max}=24{,}7\cdot\frac{U_0^2}{R_{\rm b}}\), ha \(\displaystyle n=20\) vagy \(\displaystyle n=25\).
Általában a leadott teljesítmény maximuma \(\displaystyle n_0=\sqrt{NR/R_{\rm b}}\)-nél van, ha \(\displaystyle n_0\) osztója \(\displaystyle N\)-nek, ellenkező esetben pedig \(\displaystyle N\) osztói közül a legkisebb \(\displaystyle n>n_0\) és a legnagyobb \(\displaystyle n<n_0\) valamelyikének megfelelő \(\displaystyle n\)-nél található.
Statisztika:
55 dolgozat érkezett. 5 pontot kapott: Antalicz Balázs, Asztalos Bogdán, Balogh Menyhért, Berta Dénes, Bősze Zsófia, Bugár 123 Dávid, Csathó Botond, Di Giovanni Márk, Dinev Georgi, Farkas Tamás, Fehér Zsombor, Fekete Panna, Gróf Tamás, Holczer András, Horváth Botond István, Huszár Emese, Janzer Barnabás, Juhász Péter, Kacz Dániel, Kaposvári Péter, Kovács Péter Tamás, Lőrincz Zoltán, Marosvári Kristóf, Molnár 128 Szilárd, Németh 017 András, Németh Flóra Boróka, Olosz Balázs, Öreg Botond, Radnai Bálint, Rossen Péter, Rózsa Tibor, Sal Kristóf, Seress Dániel, Szász Norbert Csaba, Szilágyi András, Tatár Dániel, Tóth Bence Tamás, Trócsányi Péter, Varju Ákos, Virágh Anna, Zarándy Álmos. 4 pontot kapott: Demeter Dániel. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 3 versenyző.
A KöMaL 2014. márciusi fizika feladatai