A P. 4631. feladat (2014. április)

P. 4631. Vízszintes, sima jégre állított kétszárú létra szárai $\displaystyle \alpha=60^\circ$-os szöget zárnak be egymással. Az $\displaystyle m=5$ kg tömegű, $\displaystyle L=2$ m hosszú szárakat összekötő csukló súrlódásmentes. A vékony, kezdetben feszes biztonsági kötél elszakad.

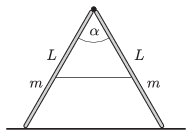
$\displaystyle a)$ Mekkora szöget zárnak be egymással a létraszárak abban a pillanatban, amikor a csukló nem fejt ki erőt?

$\displaystyle b)$ Mekkora erővel nyomja ekkor a létra a jeget?

$\displaystyle c)$ Mekkora sebességgel érkezik a jégre a csukló?

(A létraszárakat a tehetetlenségi nyomaték szempontjából tekintsük vékony, homogén rudaknak!)

Közli: Holics László, Budapest

(5 pont)

A beküldési határidő 2014. május 12-én LEJÁRT.

Megoldásvázlat. $\displaystyle a)$ $\displaystyle 2\,{\rm arccos}\left(\frac23 \cos\frac{\alpha}{2}\right)\approx 109{,}5^\circ$.

$\displaystyle b)$ $\displaystyle F= mg/2=24{,}5~$N.

$\displaystyle c)$ $\displaystyle v=\sqrt{\frac{3\sqrt{3}}{2}gL}=7{,}14~$m/s.

Statisztika:

27 dolgozat érkezett.
5 pontot kapott:	Antalicz Balázs, Asztalos Bogdán, Balogh Menyhért, Csathó Botond, Forrai Botond, Horicsányi Attila, Juhász Péter, Kovács Péter Tamás, Sal Kristóf.
4 pontot kapott:	Berta Dénes, Blum Balázs, Bugár 123 Dávid, Dinev Georgi, Elahe Ahmadi, Fehér Zsombor, Fekete Panna, Holczer András, Janzer Barnabás, Marosvári Kristóf, Németh Flóra Boróka, Olosz Balázs, Sárvári Péter.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2014. áprilisi fizika feladatai