A P. 4676. feladat (2014. november)

P. 4676. Az \(\displaystyle R\) sugarú, homogén anyageloszlású gömb sűrűsége \(\displaystyle \varrho_1\), kivéve egy kisebb, \(\displaystyle r\) sugarú, gömb alakú tartományt, amelyben a sűrűség \(\displaystyle \varrho_2\). A két gömb középpontja \(\displaystyle s\) távolságra van egymástól.

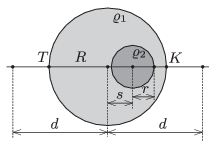
\(\displaystyle a)\) Mekkora a gravitációs gyorsulás a két gömb középpontján áthaladó egyenes mentén a nagy gömb középpontjától \(\displaystyle d\ge R\) távolságban?

\(\displaystyle b)\) Legyen \(\displaystyle s=R/2\) és \(\displaystyle r=R/4\). Ebben az esetben a gravitációs gyorsulás az ábrán látható \(\displaystyle K\) pontban 10%-kal nagyobb, mint \(\displaystyle T\)-ben. Mekkora a \(\displaystyle \varrho_2/\varrho_1\) arány?

Közli: Légrádi Imre, Sopron

(4 pont)

A beküldési határidő 2014. december 10-én LEJÁRT.

Megoldás: \(\displaystyle a)\) \(\displaystyle g=\gamma\frac{4\pi}{3} \left(\varrho_1 \frac{R^3}{d^2}+(\varrho_2-\varrho_1)\frac{r^3}{(d\mp s)^2} \right),\) ahol a második nevezőben a negatív előjel a kis gömbhöz közelebbi, a pozitív pedig a távolabbi helyzetnek felel meg.

\(\displaystyle b)\) \(\displaystyle {\varrho_2 }/{ \varrho_1}=2{,}82.\)

Statisztika:

48 dolgozat érkezett.
4 pontot kapott:	Ardai István Tamás, Asztalos Bogdán, Balogh Menyhért, Bartók Imre, Berta Dénes, Blum Balázs, Bugár 123 Dávid, Csenger Géza, Csire Roland, Di Giovanni Márk, Fehér 169 Szilveszter, Fehér Balázs, Fekete Panna, Forrai Botond, Holczer András, Jakus Balázs István, Kormányos Hanna Rebeka, Lőrincz Zoltán, Marosvári Kristóf, Molnár 157 Marcell, Olosz Balázs, Orosz Bálint, Pázmán Előd, Sal Kristóf, Szentivánszki Soma , Szépfalvi Bálint, Tomcsányi Gergely, Wiandt Péter.
3 pontot kapott:	Bencsik Bálint, Gróf Tamás, Juhász 326 Dániel, Kaposvári Péter, Körmöczi Dávid, Molnár Elizabet, Németh Flóra Boróka.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	6 versenyző.

A KöMaL 2014. novemberi fizika feladatai