A P. 4699. feladat (2015. január)

P. 4699. Egy \(\displaystyle \alpha=30^\circ\)-os hajlásszögű lejtőn két vékony lemez egy sínpárt alkot. A lemezek távolsága \(\displaystyle d=1{,}6\) cm. A sínpárra 2 cm átmérőjű golyót helyezünk, és ez csúszás nélkül legördül.

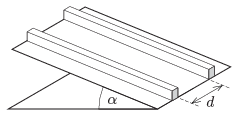
\(\displaystyle a)\) Mekkora a golyó középpontjának a gyorsulása?

\(\displaystyle b)\) \(\displaystyle \mu\) nagyságú súrlódási együttható esetén milyen meredek lejtőnél csúszik meg a golyó?

Vermes Miklós (1905-1990) feladata

(5 pont)

A beküldési határidő 2015. február 10-én LEJÁRT.

Megoldás: \(\displaystyle a)\) A gyorsulás: \(\displaystyle a=0{,}237 g\approx 2{,}4~\frac{\rm m}{\rm s^2}.\)

\(\displaystyle b)\) Akkor csúszik meg, ha a lejtő hajlásszögének tangense nagyobb, mint 3,17 \(\displaystyle \mu\).

Statisztika:

53 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Bekes Nándor, Bencsik Bálint, Blum Balázs, Csathó Botond, Fehér Balázs, Fülöp Erik, Holczer András, Iván Balázs, Kaposvári Péter, Kasza Bence, Kormányos Hanna Rebeka, Körmöczi Dávid, Lőrincz Zoltán, Öreg Botond, Varju Ákos.
4 pontot kapott:	Bugár 123 Dávid, Csenger Géza, Forrai Botond, Olosz Balázs, Szentivánszki Soma , Varga-Umbrich Eszter.
3 pontot kapott:	12 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	9 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2015. januári fizika feladatai