A P. 4701. feladat (2015. január)

P. 4701. Függőleges síkban mozgó, szigetelő anyagból készült karika \(\displaystyle P_1\) és \(\displaystyle P_2\) pontjához \(\displaystyle Q\) töltésű, kisméretű golyókat úgy, hogy \(\displaystyle \alpha=60^\circ\) (lásd az ábrát). A karika \(\displaystyle B\) indukciójú, homogén mágneses mezőben van, amelynek erővonalai merőlegesek a karika síkjára. A karikát úgy mozgatjuk, hogy az a szigetelő anyagból készült vízszintes felületen tisztán gördül, és a középpontjának sebessége \(\displaystyle v_0\).

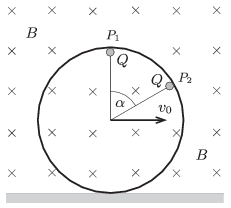
\(\displaystyle a)\) Mekkora mágneses erők hatnak az ábrán látható helyzetben az egyes töltött golyókra?

\(\displaystyle b)\) A karika mely helyzeteiben nincs a mágneses erők eredőjének forgatónyomatéka a karika középpontjára vonatkoztatva? Ezen helyzetek közül melyikben gyakorol nagyobb erőt a mágneses mező a karikára? Mekkora ez az erő?

\(\displaystyle c)\) Határozzuk meg a mágneses erők hatásvonalainak metszéspontját!

Közli: Kotek László, Pécs

(5 pont)

A beküldési határidő 2015. február 10-én LEJÁRT.

Megoldás: \(\displaystyle a)\) A \(\displaystyle P_1\) pontban lévő golyóra \(\displaystyle 2QBv_0\), a \(\displaystyle P_2\) pontban lévőre \(\displaystyle \sqrt{3}QBv_0\) nagyságú erő hat.

\(\displaystyle b)\) \(\displaystyle 150^\circ\), illetve \(\displaystyle 330^\circ\) szögelfordulás után (amikor a golyók a függőleges átmérőre szimmetrikusan helyezkednek el) a középpontra vonatkoztatott eredő forgatónyomaték nulla. Az eredő erő a golyók felső helyzeténél lesz nagyobb, értéke \(\displaystyle (2+\sqrt3)QBv_0\).

\(\displaystyle c)\) Egy-egy golyóra ható mágneses erő (a golyó tetszőleges helyzetében) a karika és a szigetelő lap érintkezési pontján halad keresztül, a két golyóra ható erők hatásvonala tehát itt, a pillanatnyi forgástengelynél metszi egymást.

Statisztika:

36 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Berta Dénes, Blum Balázs, Bugár 123 Dávid, Büki Máté, Csathó Botond, Forrai Botond, Fülöp Erik, Gróf Tamás, Holczer András, Iván Balázs, Jakus Balázs István, Kasza Bence, Kovács Péter Tamás, Lőrincz Zoltán, Marosvári Kristóf, Molnár 157 Marcell, Németh Flóra Boróka, Öreg Botond, Pázmán Előd, Sal Kristóf, Szántó Benedek, Varju Ákos, Wiandt Péter.
4 pontot kapott:	Bekes Nándor, Fehér Balázs, Fekete Panna, Kaposvári Péter, Körmöczi Dávid, Olosz Balázs, Szabó 199 Márton, Szász Norbert Csaba.
3 pontot kapott:	3 versenyző.

A KöMaL 2015. januári fizika feladatai