A P. 4734. feladat (2015. április)

P. 4734. Szigetelő anyagú, vízszintes, sima felületen három darab \(\displaystyle m\) tömegű, kisméretű, pozitív töltésű golyót \(\displaystyle L\) hosszúságú, elhanyagolható tömegű, szigetelő fonalakkal kötöttünk össze. Két golyó töltése \(\displaystyle Q\), a harmadiké pedig \(\displaystyle 2Q\). Egy adott pillanatban a \(\displaystyle Q\) töltésű golyókat összekötő fonalat elvágjuk.

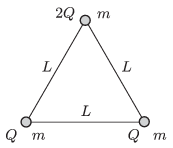
\(\displaystyle a)\) Mekkora lesz a golyók sebessége abban a pillanatban, amikor a \(\displaystyle 2Q\) töltésű golyó sebessége a legnagyobb?

\(\displaystyle b)\) Mekkora erő feszíti a fonalakat ebben a helyzetben?

\(\displaystyle c)\) Mekkora az egyes golyók elmozdulása ebben a pillanatban?

Közli: Kotek László, Pécs

(5 pont)

A beküldési határidő 2015. május 11-én LEJÁRT.

Megoldás: \(\displaystyle a)\) A \(\displaystyle 2Q\) töltésű golyó \(\displaystyle 2\sqrt{\frac{kQ^2}{6mL}}\) sebességgel, a \(\displaystyle Q\) töltésű golyók \(\displaystyle \sqrt{\frac{kQ^2}{6mL}}\) sebességgel mozognak a kérdéses pillanatban.

\(\displaystyle b)\) \(\displaystyle F=\frac{15}{4}\,\frac{kQ^2}{L^2}.\)

\(\displaystyle c)\) Mindhárom golyó elmozdulása ugyanakkora, \(\displaystyle L/\sqrt{3}\).

Statisztika:

41 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Bartók Imre, Bekes Nándor, Bencsik Bálint, Csathó Botond, Csire Roland, Csorba Benjámin, Fehér Balázs, Fekete Panna, Forrai Botond, Fülöp Erik, Holczer András, Jakus Balázs István, Kaposvári Péter, Kasza Bence, Kormányos Hanna Rebeka, Marosvári Kristóf, Németh Flóra Boróka, Öreg Botond, Pázmán Előd, Sal Kristóf, Szántó Benedek, Szentivánszki Soma , Szépfalvi Bálint.
4 pontot kapott:	Berta Dénes, Blum Balázs, Büki Máté, Kovács Péter Tamás, Körtefái Dóra, Nagy 555 Botond, Olosz Balázs, Páhoki Tamás, Radnai Bálint, Tanner Martin, Varga-Umbrich Eszter.
3 pontot kapott:	5 versenyző.

A KöMaL 2015. áprilisi fizika feladatai