A P. 4789. feladat (2015. december)

P. 4789. Vékony, egyenletes keresztmetszetű ellenálláshuzalból ún. Sierpinski-háromszöget szeretnénk forrasztani. Ehhez egy szabályos háromszög alakú keretből indulunk ki, melynek $\displaystyle A$ és $\displaystyle B$ csúcsai között $\displaystyle R_0$ ellenállást mérünk. A kerethez első lépésben hozzáforrasztjuk a háromszög középvonalait, majd második lépésben az így keletkezett négy kis háromszög közül a külső három középvonalait is beforrasztjuk. Az eljárást tovább folytatva önhasonló, fraktálszerű drótkeretet kapunk (lásd az ábrát).

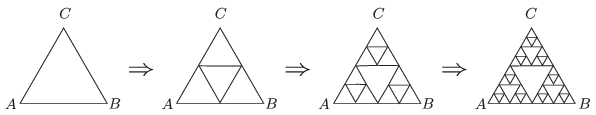
Mekkora lesz az $\displaystyle A$ és $\displaystyle B$ pontok közötti ellenállás az $\displaystyle n$-edik lépés után?

Közli: Vigh Máté, Budapest

(5 pont)

A beküldési határidő 2016. január 11-én LEJÁRT.

Megoldás. Tételezzük fel, hogy már ismerjük az $\displaystyle n$-edik lépés után kapott hálózat $\displaystyle A$ és $\displaystyle B$ közötti $\displaystyle R_n$ ellenállását. Ez a hálózat helyettesíthető egy ,,csillagkapcsolással'', amelyben a szimmetria miatt három egyforma, $\displaystyle R_n/2$ nagyságú ellenállás alkotja a csillag elemeit. A következő lépésben három ilyen, de fele méretre kicsinyített, tehát $\displaystyle R_n/4$ nagyságú elemekből álló csillagkapcsolást kötünk össze. Könnyen leolvasható, hogy ebben a lépésben

$\displaystyle R_{n+1}= \frac56R_n$

lesz az eredő ellenállás, és mivel a kiindulási értéket ismerjük,

$\displaystyle R_1=\frac56R_0,\quad R_2=\frac56R_1= \left(\frac56\right)^2R_0,\quad \ldots \quad R_n=\left(\frac56\right)^nR_0.$

Megjegyzés: A feladatban szereplő fraktálobjektumot W. F. Sierpinski (1882-1969) lengyel matematikusról nevezték el, aki többek között a halmazelméletben, a valós függvénytanban, a számelméletben és a topológiában is maradandót alkotott.

Statisztika:

33 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Blum Balázs, Csenger Géza, Di Giovanni András, Fehér 169 Szilveszter, Forrai Botond, Juhász 326 Dániel, Kasza Bence, Kovács Péter Tamás, Marozsák Tóbiás , Németh 777 Róbert, Olosz Adél, Sal Kristóf, Szentivánszki Soma , Szick Dániel, Tibay Álmos, Tófalusi Ádám, Tomcsányi Gergely, Tóth Adrián, Török Péter, Varga-Umbrich Eszter, Veres Károly, Weisz Pál, Wiandt Péter.
3 pontot kapott:	2 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2015. decemberi fizika feladatai