 |
A P. 4798. feladat (2016. január) |
P. 4798. Függőlegesen felfelé mutató, homogén elektromos mező térerősségének nagysága \(\displaystyle E\). A mezőben egy vízszintes egyenes mentén, egymástól \(\displaystyle 2a\) távolságra két rögzített, \(\displaystyle -Q\) töltés található. A töltéseket összekötő szakasz felezőpontjában függőlegesen kifeszített fonálon egy kicsiny, \(\displaystyle m\) tömegű, \(\displaystyle q>0\) töltésű gyöngyszem van (lásd az ábra \(\displaystyle a)\) részét). A gyöngyszemet (amely súrlódásmentesen tud mozogni a fonálon) álló helyzetből elengedjük. Amikor a gyöngyszem a kiindulási helyétől a legtávolabbra jut, akkor a három töltés egy olyan egyenlőszárú háromszög csúcsaiban lesz, amelynek az alappal szemközti szöge \(\displaystyle 2\alpha=150^\circ\), ahogy azt az ábra \(\displaystyle b)\) része mutatja.
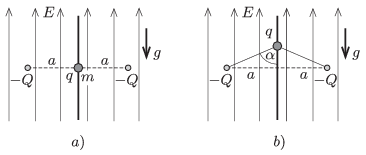
\(\displaystyle a)\) Mekkora \(\displaystyle q\)?
\(\displaystyle b)\) Mekkora lesz a gyöngyszem legnagyobb sebessége?
\(\displaystyle c)\) Legalább mekkora kezdősebességet adjunk a gyöngyszemnek, hogy a fonálon bármeddig eljuthasson?
Adatok: \(\displaystyle E=10^4~\frac{\rm N}{\rm C}\), \(\displaystyle a=10\) cm, \(\displaystyle Q=10^{-8}\) C, \(\displaystyle \alpha=75^\circ\), \(\displaystyle m=0{,}1\) g.
Közli: Zsigri Ferenc, Budapest
(5 pont)
A beküldési határidő 2016. február 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) A gyöngyszem teljes (elektrosztatikus + gravitációs) helyzeti energiája az eredeti helyzete felett \(\displaystyle x\) magasságban:
\(\displaystyle \Phi(x)=(mg-qE)x-2kqQ\left( \frac{1}{\sqrt{a^2+x^2}} - \frac 1{a}\right).\)
(Az energiát a \(\displaystyle Q\) töltésekkel azonos magasságában választottuk nullának.) Ez a kifejezés akkor lesz \(\displaystyle x=\frac{a}{{\rm tg}\,75^\circ}=0{,}0269~\)m-nél nulla, ha \(\displaystyle q=1{,}27\cdot10^{-7}~\)C.
\(\displaystyle b)\) A gyöngyszem ott éri el a legnagyobb sebességét, ahol a rá ható eredő erő nulla, vagyis ahol a potenciális energiának nulla a meredeksége. Grafikusan ábrázolva \(\displaystyle \Phi(x)\)-t leolvasható, hogy ez először \(\displaystyle x_1\approx 0{,}013\) m-nél következik be és \(\displaystyle \Phi(x_1)\approx -1{,}85\cdot10^{-6}~\)J. Ekkora helyzeti energiánál a gyöngyszem sebessége \(\displaystyle v_1\approx 0{,}2\) m/s. Az \(\displaystyle x_1\) helyen a potenciális energiának lokális minimuma van, ez tehát a gyöngyszem stabil egyensúlyi helyzete lehet.
\(\displaystyle c)\) A potenciális energiának \(\displaystyle x_2\approx 0{,}25~\)m-nél lokális maximuma van (instabil egyensúlyi helyzet) és \(\displaystyle \Phi(x_2)\approx +7{,}1\cdot10^{-5}~\)J. A gyöngyszem akkor juthat át ezen a potenciálgáton (távolodhat el tetszőleges távolságra), ha kezdetben \(\displaystyle \Phi(x_2)\)-vel megegyező mozgási energiája van, vagyis a sebessége legalább 1,2 m/s.
Statisztika:
30 dolgozat érkezett. 5 pontot kapott: Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Blum Balázs, Büki Máté, Csorba Benjámin, Fajszi Bulcsú, Forrai Botond, Iván Balázs, Kasza Bence, Kovács Péter Tamás, Körmöczi Dávid, Németh Flóra Boróka, Páhoki Tamás, Sal Kristóf, Szentivánszki Soma , Tomcsányi Gergely, Tóth Adrián. 4 pontot kapott: Fekete Balázs Attila, Kormányos Hanna Rebeka, Németh 777 Róbert, Pázmán Előd. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2016. januári fizika feladatai

