 |
A P. 4800. feladat (2016. január) |
P. 4800. Egy \(\displaystyle R\) középkörsugarú, \(\displaystyle N_1\) menetszámú toroidtekercsben \(\displaystyle I_1\) erősségű áram folyik. A toroid forgásszimmetria-tengelyében egy \(\displaystyle r\) sugarú, \(\displaystyle \ell\) hosszú (\(\displaystyle \ell\gg R\)), \(\displaystyle N_2\) menetű szolenoidot helyeztünk el. Ebben a tekercsben \(\displaystyle t_0\) idő alatt, időben egyenletesen növeljük az áramerősséget addig, amíg a toroid belsejében a mágneses tér
\(\displaystyle a)\) el nem tűnik;
\(\displaystyle b)\) ellenkezőjére változik. Mekkora az elektromos térerősség e két esetben a toroid belsejében a középkör mentén?
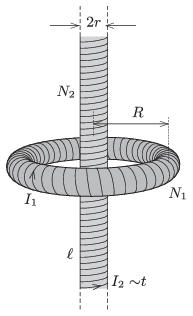
Adatok: \(\displaystyle R=20\) cm, \(\displaystyle N_1=300\), \(\displaystyle r=4\) cm, \(\displaystyle \ell=2\) m, \(\displaystyle I_1=0{,}5\) A, \(\displaystyle N_2=4000\), \(\displaystyle t_0=2\) s.
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2016. február 10-én LEJÁRT.
Megoldás. A toroid tekercs középvonalánál a mágneses indukció a saját árama miatt
\(\displaystyle B_1=\mu_0\frac{N_1I_1}{2\pi R}.\)
A szolenoid a benne folyó áram miatt a belsejében erős (\(\displaystyle N_2\)-vel arányos) mágneses teret hoz létre, de kívül sem nulla ez a tér. A szolenoidon kívül egyrészt a véges tekercshossz miatti (a tekercs tengelyével majdnem párhuzamos) szórt tér jelenik meg, másrészt a tekercs tengelye irányában folyó áramnak is van (az áramot ,,körülölelő'') mágneses tere. A toroid menetein csak ezen utóbbi, a ,,végtelen'' egyenes vezető
\(\displaystyle B_2=\mu_0\frac{I_2}{2\pi R}\)
nagyságú mágneses tere halad át, és ha elég erős, akkor a feladat ábráján látható tekercselési irányok mellett éppen kiolthatja a toroid saját mágneses terének a középkör érintőjének irányába mutató komponensét. (A szolenoid hossztengelyével majdnem párhuzamos szórt mágneses tér természetesen nem válhat nullává, hiszen a toroid mágneses indukciójának nem volt ilyen irányú komponense.) A részleges kioltás feltétele: \(\displaystyle B_1=B_2\), vagyis \(\displaystyle I_2=N_1I_1=150~\)A. Ekkora áramerősségnek megfelelő \(\displaystyle B_2\) mágneses indukció a szolenoid belsejében \(\displaystyle \Delta\Phi=B_2r^2\pi\) mágneses fluxust jelent. Ha ez a (maximális) fluxus \(\displaystyle \Delta t=2\) s alatt alakult ki a kezdeti nulla értékről, akkor a toroid középköre mentén indukálódott feszültség nagysága
\(\displaystyle U=\frac{\Delta\Phi}{\Delta t}=0{,}93~\rm mV,\)
az elektromos térerősség pedig az \(\displaystyle a)\) esetben \(\displaystyle E_a=U/(2R\pi)=0{,}75\cdot10^{-3}~\rm V/m\) lesz.
\(\displaystyle b)\) Ahhoz, hogy a toroid mágneses terének érintő irányú komponense az eredeti érték ellenkezőjére változzék, a szolenoid áramát (és ezzel együtt a mágneses terét és a gerjesztett elektromos teret is) kétszeresére kell növelni. Ilyenkor az elektromos térerősség a toroid középköre mentén \(\displaystyle E_b=2E_a= 1{,}5\cdot10^{-3}~\rm V/m\) lesz.
Statisztika:
19 dolgozat érkezett. 5 pontot kapott: Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Blum Balázs, Büki Máté, Forrai Botond, Iván Balázs, Kasza Bence, Kormányos Hanna Rebeka, Kovács Péter Tamás, Németh 777 Róbert, Sal Kristóf, Szentivánszki Soma , Tomcsányi Gergely, Zöllner András. 4 pontot kapott: Csorba Benjámin, Fekete Balázs Attila, Körmöczi Dávid, Németh Flóra Boróka.
A KöMaL 2016. januári fizika feladatai

