 |
A P. 4811. feladat (2016. február) |
P. 4811. \(\displaystyle A=10~{\rm cm}^2\) keresztmetszetű hengerben \(\displaystyle m=2~{\rm kg}\) tömegű dugattyú \(\displaystyle \ell= 30~{\rm cm}\) hosszú levegőoszlopot zár el. A külső és a belső nyomás egyaránt \(\displaystyle p_0=10^5\) Pa. A cső függőleges tengely körül foroghat. Álló helyzetben a dugattyú közepe a tengelytől \(\displaystyle r= 0{,}5\) m távolságra van.
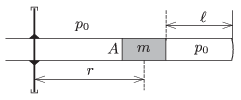
\(\displaystyle a)\) Hányszorosára változik a bezárt gáz sűrűsége, ha a csövet \(\displaystyle \omega=3~{\rm s}^{-1}\) szögsebességgel forgatjuk?
\(\displaystyle b)\) Forgás közben mekkorára kellene lecsökkennie a külső nyomásnak ahhoz, hogy a dugattyú az eredeti helyzetébe kerüljön vissza?
A hőmérséklet mindvégig állandó.
Szegedi Ervin (1956-2006) feladata
(4 pont)
A beküldési határidő 2016. március 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Ha a dugattyú \(\displaystyle x\) távolsággal elmozdul a csőben (eltávolodik a tengelytől), akkor a bezárt levegő térfogata \(\displaystyle (\ell-x)/\ell\) arányban lecsökken, az izotermikusan összenyomódott levegő nyomása tehát \(\displaystyle p_0\ell/(\ell-x)\) lesz. Másrészt a dugattyű tömegközéppontja \(\displaystyle a=(r+x)\omega^2\) gyorsulással mozog, tehát a mozgásegyenlet így írható fel:
\(\displaystyle m(r+x)\,\omega^2=Ap_0\left(\frac{\ell}{\ell-x}-1\right),\)
vagyis
\(\displaystyle (r+x)(\ell-x)=\frac{Ap_0}{m\omega^2} x.\)
Ennek a másodfokú egyenletnek (fizikailag reális, stabil helyzetnek megfelelő) megoldása: \(\displaystyle x=2{,}6~\)cm. Az ennek megfelelő helyzetben a bezárt levegő sűrűsége 9,5 százalékkal nagyobb, mint a forgatás előtti érték.
\(\displaystyle b)\) A forgó hengerben a dugattyú akkor maradhat az eredeti helyzetében, ha a külső légnyomás \(\displaystyle p_0\) értékére fennáll:
\(\displaystyle mr\omega^2=A\left(p_0-p_1\right).\)
A megadott számadatok mellett ez \(\displaystyle p_1=91~\)kPa nyomásnál teljesül.
Statisztika:
71 dolgozat érkezett. 4 pontot kapott: 53 versenyző. 3 pontot kapott: 10 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2016. februári fizika feladatai

