A P. 4816. feladat (2016. február)

P. 4816. Vízszintes síkon rögzített (végtelen hosszúnak tekinthető) vastag, egyenes vezetékben $\displaystyle I=25$ A erősségű áram folyik. A vezeték mellett, attól $\displaystyle r_0=1$ cm távolságban $\displaystyle a=5$ cm, $\displaystyle b=10$ cm oldalú, téglalap alakú, zárt, rézdrótból készített keret nyugszik a síkon. Az áramot igen rövid idő alatt egyenletesen nullára csökkentjük. Mekkora sebességre tenne szert a keret, ha nem hatna rá súrlódási erő?

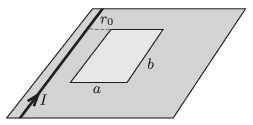
Közli: Holics László, Budapest

(5 pont)

A beküldési határidő 2016. március 10-én LEJÁRT.

Megoldás. Egyenes vezető változó erősségű árama változó indukciójú mágneses mezőt hoz létre maga körül, amelyek indukcióvonalai a vezetékkel koncentrikus körök, és merőlegesen metszik az $\displaystyle ab$ területű, téglalap alakú vezetőhurok síkját. Ebben a hurokban az általa körülvett, időben változó mágneses fluxus áramot indít, melynek $\displaystyle I_1$ nagysága a fluxus $\displaystyle \Delta t$ ideig tartó egyenletes változása miatt időben állandó. (Az áram kikapcsolásának igen rövid ideje alatt a rézkeret nem tud számottevően elmozdulni, emiatt a mágneses fluxust számíthatjuk a keret eredeti helyén.)

A vezetőhurok oldalaira ható erők időben egyenletesen változnak, így az általuk $\displaystyle t$ idő alatt létrehozott erőlökés számolható a kezdeti $\displaystyle F$ erő felének megfelelő $\displaystyle Ft/2$ átlagértékkel. Az egyenes vezetékhez közelebbi $\displaystyle b$ hosszúságú oldal mentén kialakuló mágneses indukció:

$\displaystyle B(r_0)=\frac{\mu_0}{2\pi} \frac{I}{r_0},$

a távolabbi $\displaystyle b$ oldal mentén pedig

$\displaystyle B(r_0+a)=\frac{\mu_0}{2\pi} \frac{I}{r_0+a}.$

(Az egyenes vezetékre merőleges $\displaystyle a$ hosszúságú oldalakra ható Lorentz-erők eredője az ellentétes irányú áramok és a szimmetria miatt zérus.)

A vezetőhurokra ható összes erő, ha a hurokban $\displaystyle I_1$ erősségű egyenáram folyik:

$\displaystyle F=\frac{\mu_0}{2\pi}\,\frac{II_1 ab}{r_0(r_0+a)}.$

A vezetőhurokban keletkező áram erőssége:

$\displaystyle I_1=\frac{\cal E}{R}=\frac{1}{R}\frac{\Delta\Phi}{\Delta t},$

ahol $\displaystyle R=(2a+2b)\varrho^\text{(elekt.)}/A$ az $\displaystyle A$ keresztmetszetű vezetékből készült, $\displaystyle \varrho^\text{(elekt.)}$ fajlagos ellenállású rézhuzal teljes ellenállása, $\displaystyle \Phi$ pedig a keret által körülölelt mágneses fluxus. Ez utóbbi – mivel nem homogén a vezetőhurok által körülvett mágneses mező – elemi fluxusok összegezésével számítható ki:

$\displaystyle \Phi=\sum \Delta \Phi=\sum B(r)\cdot b\Delta r=\frac{\mu_0}{2\pi}Ib\sum\limits_{r_0}^{r_0+a} \frac{\Delta r}{r}.$

Az itt szereplő összeg vagy numerikusan, vagy integrálszámítással határozható meg, de megkapható a gázok izotermikus tágulásánál végzett munka hasonló kifejezésének ismeretében is:

$\displaystyle \sum\limits_{r_0}^{r_0+a} \frac{\Delta r}{r}=\ln \left(1+\frac{a}{r_0}\right).$

A fluxusváltozás üteme tehát:

$\displaystyle \frac{\Delta\Phi}{\Delta t}=\frac{\mu_0}{2\pi}\,\frac{Ib}{\Delta t} \ln \left(1+\frac{a}{r_0}\right),$

és így – a fentebbi képleteket is felhasználva – a drótkeretre ható erő az áram csökkenésének kezdetekor:

$\displaystyle F=\left(\frac{\mu_0}{2\pi}\right)^2\,\frac{I^2}{\Delta t}\,\frac{b^2a}{r_0(r_0+a)}\, \frac{A}{2(a+b)\varrho^\text{(elekt.)}} \ln \left(1+\frac{a}{r_0}\right).$

Az átlagosan $\displaystyle F/2$ nagyságú erő $\displaystyle \Delta t$ idő alatt a $\displaystyle \varrho^\text{(mech.)}$ tömegsűrűségű, $\displaystyle m=2(a+b)A\varrho^\text{(elekt.)}$ tömegű drótkeretet

$\displaystyle v=\frac{F\Delta t}{2m}= \left(\frac{\mu_0}{2\pi}\right)^2\,\frac{I^2}{8 r_0\varrho^\text{(elekt.)} \varrho^\text{(mech.)}}\, \frac{1}{ (1+\frac{r_0}{a})(\frac{a}{b}+1)^2} \ln \left(1+\frac{a}{r_0}\right)\approx 0{,}0014~\frac{{\rm mm}}{\rm s}$

sebességre gyorsítaná fel, ha nem lenne súrlódás a síklapon. (Felhasználtuk a réz – táblázatban megtalálható fajlagos ellenállás és tömegsűrűség – adatait is.) Látható, hogy a vezeték $\displaystyle A$ keresztmetszete és az áram kikapcsolásának ideje kiesett a végképletből.

Statisztika:

27 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Blum Balázs, Büki Máté, Fekete Balázs Attila, Forrai Botond, Ghada Alshalan, Iván Balázs, Jakus Balázs István, Kasza Bence, Kovács Péter Tamás, Sal Kristóf, Szentivánszki Soma , Szick Dániel, Tomcsányi Gergely, Zöllner András.
4 pontot kapott:	Csorba Benjámin, Körmöczi Dávid, Mándoki László, Németh 777 Róbert, Páhoki Tamás.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2016. februári fizika feladatai