A P. 4852. feladat (2016. május)

P. 4852. Függőleges, mindkét végén zárt, \(\displaystyle A=1~{\rm dm}^2\) keresztmetszetű, hőszigetelt hengerben lévő, súrlódásmentesen mozgó dugattyút a henger két végével két húzó-nyomó rugó köt össze. A rugók nyújtatlan hossza \(\displaystyle \ell_1=3~{\rm dm}\) és \(\displaystyle \ell_2=5~{\rm dm}\), a direkciós erejük pedig \(\displaystyle D_1=1000\) N/m és \(\displaystyle D_2=1500\) N/m. A dugattyú alatt levegő van, amelynek nyomása kezdetben \(\displaystyle p_1=4\cdot10^4\) Pa, a dugattyú felett pedig vákuum van. Kezdetben a dugattyú távolsága a henger végeitől \(\displaystyle d_1=5~{\rm dm}\) és \(\displaystyle d_2=4~{\rm dm}\).

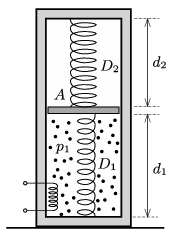
\(\displaystyle a)\) Határozzuk meg a dugattyú tömegét!

\(\displaystyle b)\) A levegőt lassan melegítjük. Hányszorosára kell növelni a gáz Kelvin-skálán mért hőmérsékletét, hogy a dugattyú felfelé 10 cm-rel elmozduljon?

\(\displaystyle c)\) Mennyi hőt közültünk a gázzal a melegítés során?

Közli: Kotek László, Pécs

(5 pont)

A beküldési határidő 2016. június 10-én LEJÁRT.

Megoldás. \(\displaystyle a)\) A rugók által kifejtett erők:

\(\displaystyle F_1=D_1(d_1-\ell_1)=200~{\rm N}~ \text{(lefelé ható húzóerő)},\)

\(\displaystyle F_2=D_2(d_2-\ell_2)=-150~{\rm N}~ \text{(lefelé ható nyomóerő)}. \)

A gáz által kifejtett (felfelé ható) erő:

\(\displaystyle F_3=p_1 A=400~\rm N.\)

A dugattyúra ható nehézségi erő:

\(\displaystyle G=F_3-F_1-\vert F_2\vert=50~{\rm N},\)

tehát a dugattyú tömege

\(\displaystyle m=\frac{G}{g}\approx 5~\rm kg.\)

\(\displaystyle b)\) Ha a dugattyú \(\displaystyle s=0{,}1\) m-t elmozgul felfelé, akkor a rugók által kifejtett erő megnő

\(\displaystyle \Delta F=(D_1+D_2)s=250~\rm N\)

értékkel. A gáz nyomásának változása

\(\displaystyle \Delta p=\frac{\Delta F}{A}=2{,}5\cdot10^4~\rm Pa,\)

a levegő nyomása tehát \(\displaystyle p_2=6{,}5\cdot10^4\) Pa lesz.

A gáztörvény szerint az abszolút hőmérsékletek aránya:

\(\displaystyle \frac{T_2}{T_1}=\frac{p_2}{p_1}\cdot \frac{d_1+s}{d_1}= \frac{6{,}5}{4{,}0}\cdot \frac{6}{5}=1{,}95.\)

\(\displaystyle c)\) A közölt hő a levegő belső energiájának növekedését, a dugattyú helyzeti energiájának növekedését és a rugók rugalmas energiájának megváltozását hozza létre.

A belső energia megváltozása:

\(\displaystyle \Delta E_1=\frac{5}{2}p_2V_2-\frac{5}{2}p_1V_1=475~\rm J.\)

A dugattyú helyzeti energiájának növekedése:

\(\displaystyle \Delta E_1=mgs=50~{\rm N}\cdot 0{,}1~{\rm m}=5~{\rm J}.\)

A rugók energiaváltozása:

\(\displaystyle \Delta E_3=\frac{1}{2}D_1(d_1-\ell_1+s)^2-\frac{1}{2}D_1(d_1-\ell_1)^2=25~{\rm J},\)

illetve

\(\displaystyle \Delta E_4=\frac{1}{2}D_2(d_2-\ell_2-s)^2-\frac{1}{2}D_1(d_2-\ell_1)^2=22{,}5~{\rm J}.\)

A közölt hő:

\(\displaystyle Q=\Delta E_1+\Delta E_2+\Delta E_3+\Delta E_4=527{,}5~{\rm J}.\)

(Látható, hogy a hő legnagyobb részben a levegő felmelegítésére fordítódott.)

Statisztika:

48 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Büki Máté, Csorba Benjámin, Édes Lili, Fajszi Bulcsú, Fehér 169 Szilveszter, Forrai Botond, Ghada Alshalan, Iván Balázs, Jakus Balázs István, Kovács Péter Tamás, Körmöczi Dávid, Krasznai Anna, Marozsák Tóbiás , Molnár Mátyás, Németh Flóra Boróka, Olosz Adél, Páhoki Tamás, Sal Kristóf, Sallai Krisztina, Szántó Benedek, Szentivánszki Soma , Tibay Álmos, Tomcsányi Gergely.
4 pontot kapott:	Bartók Imre, Bekes Nándor, Berke Martin, Csire Roland, Csuha Boglárka, Di Giovanni András, Farkas Domonkos, Fekete Balázs Attila, Kavas Katalin, Kormányos Hanna Rebeka, Kovács 526 Tamás, Mány Bence, Németh 777 Róbert, Pataki 245 Attila, Pázmán Előd, Pszota Máté, Simon Dániel Gábor, Tófalusi Ádám, Varga-Umbrich Eszter, Wiandt Péter.
3 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2016. májusi fizika feladatai