A P. 4860. feladat (2016. szeptember)

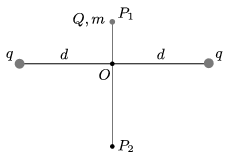
P. 4860. Két rögzített, \(\displaystyle q\) nagyságú pontszerű töltés egy \(\displaystyle 2d\) hosszúságú, vízszintes szakasz két végpontjában helyezkedik el. A szakasz függőleges felezőmerőlegesén lévő \(\displaystyle P_1\) pontból elejtünk egy \(\displaystyle m\) tömegű, \(\displaystyle Q\) töltésű golyót. A golyó a \(\displaystyle P_2\) pontban éppen megáll.

\(\displaystyle a)\) Mekkora a golyó tömege?

\(\displaystyle b)\) Mekkora a golyó gyorsulása a \(\displaystyle P_2\) pontban?

Adatok: \(\displaystyle q=2\cdot10^{-6}\) C, \(\displaystyle Q=-6\cdot10^{-6}\) C, \(\displaystyle d=12\) cm, \(\displaystyle OP_1=5\) cm, \(\displaystyle OP_2=10\) cm.

Szilárd Leó fizikaverseny, Szekszárd

(4 pont)

A beküldési határidő 2016. október 10-én LEJÁRT.

Megoldás. \(\displaystyle a)\) A golyó távolsága a töltésektől kezdetben \(\displaystyle r_1= 0{,}13\) m, a \(\displaystyle P_2\) pontban pedig \(\displaystyle r_2=0{,}156\) m. A golyó \(\displaystyle h=0{,}15\) m-nyi süllyedése során a gravitációs és az elektrosztatikus energiaváltozásának összege (a munkatétel szerint) nulla, így

\(\displaystyle 2kQq\left(\frac{1}{r_2}-\frac{1}{r_2}\right)-mgh=0.\)

Innen a megadott számadatokkal \(\displaystyle m=0{,}19~\)kg.

\(\displaystyle b)\) A \(\displaystyle P_2\) pontban függőlegesen felfelé ható erő:

\(\displaystyle F=2kq\vert Q\vert \frac{H}{r_2^3}-mg,\)

ahol \(\displaystyle H=OP_2=0{,}1~\)m. Innen a már kiszámított tömeg ismeretében a gyorsulás (felfelé):

\(\displaystyle a=\frac{F}{m}= 20{,}1~ {\rm m}/{\rm s^2}.\)

Statisztika:

74 dolgozat érkezett.
4 pontot kapott:	Ardai István Tamás, Balaskó Dominik, Balog 518 Lóránd, Bartók Imre, Bekes Nándor, Berke Martin, Csenger Géza, Csire Roland, Csóka987 Benedek, Csuha Boglárka, Debreczeni Tibor, Di Giovanni András, Édes Lili, Elek Péter, Eper Miklós, Facskó Benedek, Faisal Fahad AlSallom, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Guba Zoltán, Hanusz Fruzsina, Illés Gergely, Illyés András, Iván Balázs, Jáger Balázs, Jakus Balázs István, Kolontári Péter, Krasznai Anna, Markó Gábor, Marozsák Tóbiás , Merkl Gergely, Mocskonyi Mirkó, Molnár 957 Barnabás, Németh 123 Balázs, Nenezic Patrick Uros, Ónodi Gergely, Osváth Botond, Páhoki Tamás, Papp 121 Krisztina, Paulovics Péter, Pszota Máté, Riskutia Balázs, Schmera Dániel, Tibay Álmos, Tófalusi Ádám, Tóth 111 Máté , Tóth 420 Péter, Zöllner András, Zsombó István.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2016. szeptemberi fizika feladatai