A P. 4885. feladat (2016. december)

P. 4885. Két dobozt egymásra helyezünk az ábrán látható módon, majd elengedjük egy \(\displaystyle \alpha\) hajlásszögű lejtőn. A két (homogén tömegeloszlású) doboz között elegendően nagy a súrlódás ahhoz, hogy ne csússzanak egymáson, de a két doboz együtt lecsúszik a \(\displaystyle \mu\) súrlódási együtthatójú lejtőn.

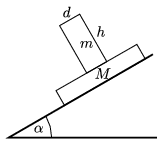
Mi a feltétele annak, hogy a felső doboz ne boruljon fel?

Közli: Takács László, Baltimore, USA

(5 pont)

A beküldési határidő 2017. január 10-én LEJÁRT.

I. megoldás. A két doboz egyetlen testként \(\displaystyle a=g(\sin\alpha-\mu \cos\alpha)\) gyorsulással lefelé mozog a lejtőn. A \(\displaystyle m\) tömegű dobozra a függőlegesen lefelé mutató, \(\displaystyle mg\) nagyságú nehézségi erő, a lejtővel párhuzamos \(\displaystyle S\) súrlódási erő és a lejtőre merőleges \(\displaystyle N\) nyomóerő hat. A mozgásegyenletek (lejtő irányában és arra merőlegesen):

\(\displaystyle mg\sin\alpha-S=ma,\qquad mg\cos\alpha-N=0,\)

ahonnan a gyorsulás ismert értékét behelyettesítve

\(\displaystyle S=\mu mg\cos\alpha, \qquad N=mg\cos\alpha.\)

A felső doboz nem jön forgásba, emiatt a rá ható erők eredő forgatónyomatéka a tömegközéppontjára nézve nulla kell legyen:

\(\displaystyle N\,d'-S\,\frac{h}{2}=0, \qquad \text{azaz} \qquad \mu=\frac{2d'}{h}.\)

Mivel az \(\displaystyle N\) erő hatásvonala legfeljebb \(\displaystyle d/2\) távolságban lehet a felső doboz (tömeg)középpontjától (\(\displaystyle d'\le d/2\)), fenn kell álljon, hogy \(\displaystyle d\ge\mu h\).

II. megoldás. Írjuk fel a felső doboz egyensúlyának feltételét a dobozzal együtt mozgó koordináta-rendszerben. Ebben a gyorsuló rendszerben fellép egy \(\displaystyle ma=mg\sin\alpha-\mu mg\cos\alpha\) nagyságú, a lejtő mentén felfelé mutató tehetetlenségi erő, amelynek a támadáspontja (éppúgy, mint a nehézségi erőé) a test tömegközéppontja. Az eredő erő lejtő irányú komponense \(\displaystyle \mu mg\cos\alpha\), a lejtőre merőleges összetevő pedig \(\displaystyle mg\cos\alpha\). Az eredő erő hatásvonala akkor esik a két doboz érintkezési felületére (akkor nem billen fel a felső doboz), ha fennáll, hogy

\(\displaystyle \frac{\mu mg\cos\alpha}{ mg\cos\alpha}=\mu \le\frac{d}{h}.\)

Megjegyzés. Érdekes, hogy a fel nem borulás feltétele sem a dobozok tömegétől, sem a lejtő hajlásszögétől nem függ. Ha a súrlódás nagyon kicsi, akkor még egy nagyon ,,karcsú'' (\(\displaystyle d\ll h\)) doboz sem borul fel, miközben csúszik lefelé egy (akár nagyon meredek) lejtőn.

Statisztika:

50 dolgozat érkezett.
5 pontot kapott:	Bartók Imre, Bekes Nándor, Csire Roland, Csuha Boglárka, Elek Péter, Fehér 169 Szilveszter, Fekete Balázs Attila, Illés Gergely, Iván Balázs, Klučka Vivien, Köpenczei Csenge, Krasznai Anna, Marozsák Tóbiás , Molnár Mátyás, Morvai Orsolya, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Ónodi Gergely, Páhoki Tamás, Pataki 245 Attila, Paulovics Péter, Sal Dávid, Szalay Gergő, Tófalusi Ádám, Tóth 111 Máté , Vígh Márton.
4 pontot kapott:	Kondákor Márk, Magyar Máté, Szentivánszki Soma , Varga-Umbrich Eszter.
3 pontot kapott:	9 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2016. decemberi fizika feladatai