 |
A P. 4903. feladat (2017. január) |
P. 4903. Felül rögzített, \(\displaystyle L\) hosszúságú, elhanyagolható tömegű, szigetelő anyagból készített fonál alsó végére egy kis méretű, \(\displaystyle m\) tömegű, \(\displaystyle Q\) töltésű golyót rögzítünk. A fonál és a golyó alkotta rendszer homogén mágneses mezőben van, \(\displaystyle \boldsymbol B\) az ábra síkjára merőlegesen befelé mutat.
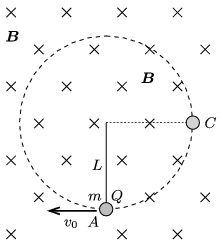
A golyót a fonálra és a mágneses indukcióvektorra merőlegesen elindítjuk. Megfelelő kezdősebesség esetén a golyó úgy halad végig a körpályáján, hogy a fonál mindvégig feszes marad.
\(\displaystyle a)\) Mekkora a \(\displaystyle B\) mágneses indukció értéke, ha az ilyen mozgáshoz szükséges legkisebb kezdősebesség \(\displaystyle v_0=\frac 12 \sqrt{17Lg}\,\)?
\(\displaystyle b)\) Ilyen kezdősebesség mellett hányszor nagyobb a fonalat feszítő erő az \(\displaystyle A\) pontban, mint amikor a test a \(\displaystyle C\) pontban van?
Közli: Kotek László, Pécs
(5 pont)
A beküldési határidő 2017. február 10-én LEJÁRT.
Megoldás. A mágneses Lorentz-erő merőleges a test sebességére (így nem végez munkát), iránya \(\displaystyle Q>0\) és a megadott irányú mágneses indukció és sebesség esetén ,,kifelé'' mutat. Amikor a fonál \(\displaystyle \alpha\) szöget zár be a függőlegessel, a golyó sebessége (az energiamegmaradás törvénye szerint)
\(\displaystyle v=\sqrt{v_0^2-2Lg(1-\cos\alpha)},\)
éppen ugyanakkora, mint amekkora mágneses tér nélküli esetben lenne. A megadott nagyságú \(\displaystyle v_0\) mellett a sebesség így is felírható:
\(\displaystyle v(\alpha)=\frac{3}{2}\sqrt{Lg}\sqrt{1+\frac{8}{9}\cos\alpha}.\)

A test mozgásegyenlete (pontosabban annak sugár irányú komponense) az ábrán látható helyzetben:
\(\displaystyle K-mg\cos\alpha-QvB=\frac{mv^2}{L},\)
amibe \(\displaystyle v(\alpha)\) fentebb kiszámított kifejezését beírva a fonalat feszítő erőre a
\(\displaystyle K(\alpha)=mg\left( 3\cos\alpha+\frac{9}{4}+\frac{QB}{2mg}\sqrt{Lg(9+8\cos\alpha)}\right) \)
kifejezést kapjuk. Ez a függvény a \(\displaystyle 0<\alpha<180^\circ\) intervallumban monoton csökken, tehát ha még a pálya tetőpontján \(\displaystyle \alpha=180^\circ\)-nál sem válik negatívvá, akkor a körpálya más részén sem lazulhat meg a fonál.
\(\displaystyle a)\) Mivel \(\displaystyle v_0\) megadott értéke az a legkisebb kezdősebesség, amellyel indítva a testet a fonál még éppen nem lazul meg sehol, ebben a határesetben \(\displaystyle K(180^\circ)=0\) teljesül. Eszerint a mágneses indukció nagysága
\(\displaystyle B=\frac{3}{2}\,\frac{mg}{Q\sqrt{Lg}},\)
és a fonalat feszítő erő tetszőleges helyzetben
\(\displaystyle K(\alpha)=mg\left( 3\cos\alpha+\frac{9}{4}+\frac{3}{4}\sqrt{9+8\cos\alpha}\right). \)
\(\displaystyle b)\) A fonálerő a \(\displaystyle C\) pontban (\(\displaystyle \alpha=0\) esetén)
\(\displaystyle K_A=\frac{21+3\sqrt{17}}{4}mg\approx 8{,}3\,mg,\)
a \(\displaystyle C\) pontban (\(\displaystyle \alpha=90^\circ\)-os szögnél) pedig
\(\displaystyle K_C=\frac{9}{2}\,mg=4{,}5\,mg,\)
a kérdezett arány tahát
\(\displaystyle \frac{K_A}{K_C}=\frac{21+3\sqrt{17}}{18}\approx 1{,}8.\)
Statisztika:
54 dolgozat érkezett. 5 pontot kapott: Csuha Boglárka, Di Giovanni András, Faisal Fahad AlSallom, Fekete Balázs Attila, Ghada Alshalan, Illés Gergely, Jakus Balázs István, Kolontári Péter, Krasznai Anna, Makovsky Mihály, Marozsák Tóbiás , Németh 123 Balázs, Zöllner András. 4 pontot kapott: Bartók Imre, Bekes Nándor, Bukor Benedek, Csire Roland, Elek Péter, Eper Miklós, Fajszi Bulcsú, Fehér 169 Szilveszter, Guba Zoltán, Illyés András, Kondákor Márk, Kormányos Hanna Rebeka, Magyar Róbert Attila, Molnár Mátyás, Nagy 555 Botond, Németh 777 Róbert, Németh Csaba Tibor, Olosz Adél, Páhoki Tamás, Papp 121 Krisztina, Pataki 245 Attila, Sugár Soma, Szentivánszki Soma , Tófalusi Ádám, Tóth 111 Máté . 3 pontot kapott: 7 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. januári fizika feladatai
