A P. 4904. feladat (2017. január)

P. 4904. Az ábrán látható kapcsolásban a $\displaystyle C$ kapacitású kondenzátor feszültsége kezdetben $\displaystyle 2U_0$, a $\displaystyle 2C$ kapacitású kondenzátor töltetlen.

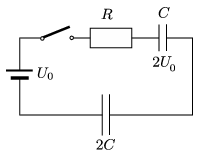
Mennyi hő fejlődik az $\displaystyle R$ ellenálláson, miután zártuk a kapcsolót?

Közli: Szász Krisztián, Budapest

(6 pont)

A beküldési határidő 2017. február 10-én LEJÁRT.

Megoldás. A kapcsoló zárása után az ellenálláson (időben változó nagyságú) áram folyik keresztül, ennek az áramnak a hőhatására vagyunk kiváncsiak. A Joule-hő például az időben változó $\displaystyle P=I^2R$ teljesítmény integrálásával határozható meg, de elemi úton, az energiaviszonyok megvizsgálásával is kiszámítható.

Tudjuk, hogy a $\displaystyle C$ kapacitású kondenzátor feszültségének nagysága $\displaystyle 2U_0$, de a feszültség előjele nem derül ki a feladat szövegéből. Emiatt meg kell vizsgálnunk mindkét polaritás lehetőségét.

$\displaystyle a)$ Legyen a $\displaystyle C$ kapacitású (a rajzon felső) kondenzátor jobb oldali lemeze kezdetben $\displaystyle +2CU_0$ töltésű, a bal oldali lemez töltése ennek $\displaystyle (-1)$-szerese. A másik (alsó) kondenzátor töltetlen. A kapcsoló zárása után a felső kondenzátor átad valamekkora $\displaystyle \Delta Q$ töltést az alsó kondenzátornak, így a töltésük $\displaystyle 2CU_0-\Delta Q$, illetve $\displaystyle \Delta Q$ lesz. Kirchhoff II. törvénye szerint az áramkörben a körfeszültség nulla:

$\displaystyle U_0+\frac{2CU_0-\Delta Q}{C}-\frac{\Delta Q}{2C}=0,$

ahonnan kiszámítható az átadott töltés:

$\displaystyle \Delta Q=2CU_0.$

Ugyanekkora töltés kerül a felső kondenzátor bal oldali lemezére, ezt a telep adja le. Végeredményben a felső kondenzátor elveszíti az összes töltését, az alsó pedig $\displaystyle 2CU_0$ töltéssel feltöltődik.

A két kondenzátor elektrosztatikus összenergiája kezdetben

$\displaystyle {\cal E}_1=\frac{1}{2}\frac{(2CU_0)^2}{C}+0=2CU_0^2$

volt. A kapcsoló zárása után kialakult helyzetben a kondenzátorok összenergiája:

$\displaystyle {\cal E}_2=0+\frac{1}{2}\frac{(2CU_0)^2}{2C}=CU_0^2.$

Az elektrosztatikus energia megváltozása:

$\displaystyle \Delta {\cal E}_\text{kondenzátor}={\cal E}_2-{\cal E}_1= -CU_0^2.$

Ne feledkezzünk meg arról sem, hogy a két kondenzátor csak a teleppel együtt alkot zárt rendszert, és a folyamat során a telep energiája is megváltozik, hiszen lead $\displaystyle \Delta Q$ töltést:

$\displaystyle \Delta {\cal E}_\text{telep}=-U_0\Delta Q=-2CU_0^2.$

A rendszer teljes energiájának csökkenése az ellenálláson fejlődő $\displaystyle W$ hővel egyenlő:

$\displaystyle W=-\Delta {\cal E}_\text{kondenzátor}-\Delta {\cal E}_\text{telep}=+3CU_0^2.$

$\displaystyle b)$ Hasonló módon számolhatjuk ki a másik polaritással feltöltött kondenzátor esetét is. Ha a felső kondenzátor jobb oldali lemezén kezdetben $\displaystyle -2CU_0$ töltés van, a kapcsoló zárása után eltávozik róla $\displaystyle \Delta Q$ töltés, akkor a huroktörvény szerint

$\displaystyle U_0+\frac{-2CU_0-\Delta Q}{C}-\frac{\Delta Q}{2C}=0.$

Innen következik, hogy

$\displaystyle \Delta Q=-\frac{2}{3}CU_0,$

a felső kondenzátor jobb oldali lemezének töltése tehát $\displaystyle -\frac{4}{3}CU_0$-ra, az alsó kondenzátor töltése pedig $\displaystyle \pm \frac{2}{3}CU_0$-ra változik.

Az energiaviszonyok változása most így alakul:

$\displaystyle \Delta {\cal E}_\text{kondenzátor}={\cal E}_2-{\cal E}_1= \frac12 \left(\frac{16}{9}+\frac{4}{9}\frac{1}{2}-4\right)CU_0^2=-CU_0^2,$

vagyis ugyanannyi, mint az előző esetben, de a telep energiaváltozása

$\displaystyle \Delta {\cal E}_\text{telep}=-U_0\Delta Q=\frac23CU_0^2.$

(A telep most felvesz töltéseket, emiatt az energiája növekszik.)

A fejlődő hő ebben az esetben

$\displaystyle W=-\Delta {\cal E}_\text{kondenzátor}-\Delta {\cal E}_\text{telep}=+\frac13CU_0^2.$

Megjegyzés. Belátható, hogy ha egy ellenálláson időben exponenciálisan csökkenő áram folyik keresztül (esetünkben éppen ez történik), akkor a kisülési folyamat során fejlődő teljes Joule-hő az ellenállásra eső kezdeti (maximális) feszültség és az ellenálláson átfolyó töltés szorzatának felével egyezik meg. A feladatban szereplő kapcsolásnál ez

$\displaystyle \tfrac12 (3U_0)(2CU_0)=3CU_0^2,\qquad \text{illetve}\qquad \tfrac12 (-U_0)(-\tfrac23CU_0)=\tfrac13CU_0^2.$

Statisztika:

26 dolgozat érkezett.
6 pontot kapott:	Elek Péter, Fehér 169 Szilveszter, Fekete Balázs Attila, Jakus Balázs István, Marozsák Tóbiás , Nagy 555 Botond, Németh 777 Róbert, Olosz Adél, Sal Dávid, Szentivánszki Soma .
5 pontot kapott:	Bekes Nándor, Kolontári Péter, Németh 123 Balázs, Tófalusi Ádám.
4 pontot kapott:	5 versenyző.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2017. januári fizika feladatai