 |
A P. 4921. feladat (2017. március) |
P. 4921. Vízszintes, mindkét végén zárt hengerben lévő, súrlódásmentesen mozgó dugattyúk \(\displaystyle p_0=10^4\) Pa nyomású, \(\displaystyle V_0=2~\rm dm^3\) térfogatú, azonos hőmérsékletű és anyagi minőségű, kétatomos ideális gázokat zárnak el. A dugattyúkat egy olyan rugó köti össze, melynek nyújtatlan hossza a henger hosszával azonos. A dugattyúk között vákuum van.
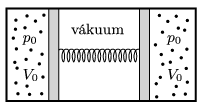
\(\displaystyle a)\) Mekkora a rugóban tárolt energia ebben az állapotban?
\(\displaystyle b)\) A gázokat egy adott pillanatban azonos módon, lassan melegíteni kezdjük, és az abszolút hőmérsékletüket a háromszorosára növeljük. Mekkora lesz a gázok nyomása a melegítés után?
\(\displaystyle c)\) Mennyi hőt kellett közölni a rendszerrel, ha a veszteségektől eltekintünk?
Közli: Kotek László, Pécs
(5 pont)
A beküldési határidő 2017. április 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Legyen a dugattyúk keresztmetszete \(\displaystyle A\), akkor mindkét dugattyú \(\displaystyle x=V_0/A\) távol van a henger közelebbi végétől. Ha a rugó rugóállandója \(\displaystyle D\), akkor \(\displaystyle 2x\) összenyomódás mellett
\(\displaystyle 2\frac{V_0}{A}D=p_0A\)
erőt fejt ki a dugattyúkra. Eszerint a rugóállandó
\(\displaystyle D=\frac{p_0 A^2}{2V_0}. \)
A rugóban tárolt rugalmas energia ebben az állapotban
\(\displaystyle W=\frac{1}{2}D(2x)^2=\frac{1}{2}D\left(2\frac{V_0}{A}\right)^2=p_0V_0=20~\rm J. \)
\(\displaystyle b)\) Ha a melegítés hatására a gázok térfogata \(\displaystyle V_1\)-re, a nyomásuk \(\displaystyle p_1\)-re, a rugó összenyomódása pedig \(\displaystyle 2x_1=2\frac{V_1}{A}\)-ra nő, a dugattyúkra ható erők egyensúlyának feltétele:
\(\displaystyle p_1A=2D\frac{V_1}{A},\)
amit a kezdeti állapot egyensúlyi egyenletével összevetve kapjuk, hogy
\(\displaystyle V_1 =\frac{p_1}{p_0}V_0.\)
Másrészt a gáztörvény szerint
\(\displaystyle p_1V_1= \frac{p_1^2}{p_0}V_0 =3p_0V_0,\)
és így
\(\displaystyle p_1=\sqrt{3}p_0=1{,}73\cdot10^4~\rm Pa.\)
\(\displaystyle c)\) A gázokkal közölt hő az I. főtétel szerint
\(\displaystyle Q=\Delta E_\text{belső}+\Delta W_\text{rugó}=2\cdot \frac{5}{2}\left(p_1V_1-p_0V_0\right)+p_1V_1-p_0V_0=12\,p_0V_0=240~\rm J.\)
Statisztika:
61 dolgozat érkezett. 5 pontot kapott: Balog 518 Lóránd, Bekes Nándor, Bíró Dániel, Bukor Benedek, Csire Roland, Csuha Boglárka, Édes Lili, Elek Péter, Fajszi Bulcsú, Fehér 169 Szilveszter, Guba Zoltán, Illés Gergely, Klučka Vivien, Kondákor Márk, Kozák András, Krasznai Anna, Marozsák Tóbiás , Molnár Mátyás, Morvai Orsolya, Németh 777 Róbert, Olosz Adél, Ónodi Gergely, Pszota Máté, Sal Dávid, Tófalusi Ádám, Tóth 111 Máté , Zöllner András. 4 pontot kapott: Bartók Imre, Debreczeni Tibor, Fekete Balázs Attila, Jáger Balázs, Kolontári Péter, Magyar Róbert Attila, Nagy 555 Botond, Németh 123 Balázs, Páhoki Tamás, Richlik Róbert, Szakály Marcell, Szentivánszki Soma , Turcsányi Ádám, Varga-Umbrich Eszter. 3 pontot kapott: 14 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. márciusi fizika feladatai

