 |
A P. 4922. feladat (2017. március) |
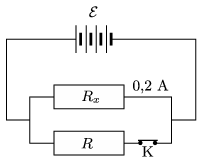
P. 4922. Egy telep elektromotoros ereje \(\displaystyle \mathcal{E}= 18\) V. A párhuzamosan kapcsolt egyik, \(\displaystyle R_x\) ellenállású fogyasztón 0,2 A erősségű áram folyik, a másik fogyasztó ellenállása \(\displaystyle R=8~\Omega\). Ha ezt a fogyasztót a K kapcsoló nyitásával kiiktatjuk, az áram erőssége az \(\displaystyle R_x\) ellenálláson 0,3 A-re nő. Mekkora a fogyasztó ellenállása és a telep belső ellenállása?
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2017. április 10-én LEJÁRT.
Megoldás. Jelöljük a telep belső ellenállását \(\displaystyle r\)-rel! A nyitott kapcsolóálláshoz tartozó Ohm-tövény (az SI mértékegységek elhagyásával):
\(\displaystyle (R_x+r)\cdot 0{,}3=18,\)
vagyis
| \(\displaystyle (1)\) | \(\displaystyle R_x+r=60. \) |
Zárt kapcsolóállás esetén az ismeretlen ellenálláson \(\displaystyle 0{,}2\,R_x\) feszültség esik, tehát a 8 ohmos ellenálláson \(\displaystyle 0{,}025\,R_x\) áram folyik. A teljes áramkörre felírható Ohm-törvény:
| \(\displaystyle (2)\) | \(\displaystyle \left(0{,}2+0{,}025\,R_x\right)r+0{,}2\,R_x=18.\) |
Az (1) egyenletből kifejezhető \(\displaystyle r\)-et (2)-be helyettesítve az ismeretlen ellenállásra egy másodfokú egyenletet kapunk:
\(\displaystyle R_x^2-60\,R_x+240=0,\)
amelynek gyökei:
\(\displaystyle R_x=55{,}7~\Omega \qquad \text{vagy} \qquad R_x=4{,}3~\Omega.\)
A telep belső ellenállása (1) szerint \(\displaystyle r=4{,}3~\Omega\) vagy \(\displaystyle r=55{,}7~\Omega\). (A második érték irreálisan nagy, emiatt azt – jóllehet a megadott feltételeknek matematikailag megfelel – elvethetjük.)
Megjegyzés. A kapcsoló nyitásával a főág áramerőssége lecsökken (hiszen a két párhuzamosan kapcsolt ág eredő ellenállása megnő), az \(\displaystyle R_x\) ellenálláson folyó áram nagysága azonban – érdekes módon – megnő.
Statisztika:
62 dolgozat érkezett. 5 pontot kapott: Balaskó Dominik, Bartók Imre, Bekes Nándor, Bukor Benedek, Csire Roland, Di Giovanni András, Édes Lili, Elek Péter, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Illés Gergely, Jakus Balázs István, Jánosik Áron, Keltai Dóra, Kolontári Péter, Kondákor Márk, Kozák András, Krasznai Anna, Magyar Róbert Attila, Mamuzsics Gergő Bence, Marozsák Tóbiás , Molnár Mátyás, Nagy 555 Botond, Németh 777 Róbert, Nyerges Dóra, Olosz Adél, Ónodi Gergely, Osváth Botond, Páhoki Tamás, Papp 121 Krisztina, Pataki 245 Attila, Póta Balázs, Pszota Máté, Sal Dávid, Sugár Soma, Szakály Marcell, Szentivánszki Soma , Tófalusi Ádám, Varga-Umbrich Eszter, Wesniczky Albert, Zöllner András, Zsombó István. 4 pontot kapott: 10 versenyző. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 4 versenyző.
A KöMaL 2017. márciusi fizika feladatai

