A P. 4928. feladat (2017. április)

P. 4928. $\displaystyle a)$ Mekkora gyorsulással indulnak meg az ábrán látható, könnnyen gördülő kiskocsik, ha a csiga tömege és a légellenállás elhanyagolható? Adatok: $\displaystyle m_1=1$ kg, $\displaystyle m_2=2$ kg, $\displaystyle M=5$ kg.

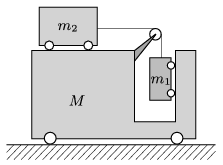
$\displaystyle b)$ Milyen határok közé eshet az $\displaystyle M$ tömegű kiskocsi kezdeti gyorsulása más tömegadatok mellett?

Közli: Németh László, Fonyód

(5 pont)

A beküldési határidő 2017. május 10-én LEJÁRT.

Megoldás. Jelöljük a testekre ható erőket és a testek gyorsulását az ábrán látható módon! (Az $\displaystyle m_2$ tömegű kiskocsi a $\displaystyle M$ tömegű kocsikoz képest $\displaystyle a$, a talajhoz képest tehát $\displaystyle a-A$ gyorsulással mozog.)

A mozgásegyenletek:

$\displaystyle m_1g-K=m_1a,$

$\displaystyle K-F=MA,$

$\displaystyle K=m_2(a-A),$

$\displaystyle F=m_1A.$

Az egyenletrendszer megoldása:

$\displaystyle A=\frac{m_1m_2}{m_1\left(m_1+m_2+M\right)+m_2\left(m_1+M\right) }\,g,$

$\displaystyle a=\frac{m_1\left(m_1+m_2+M\right) }{m_1\left(m_1+m_2+M\right)+m_2\left(m_1+M\right) }\,g.$

$\displaystyle a)$ A megadott tömegek esetén

$\displaystyle A=\frac{1}{10}g=0{,}98~\frac{\rm m}{\rm s^2}\approx 1{,}0 ~\frac{\rm m}{\rm s^2},$

$\displaystyle a=\frac{2}{5}g=3{,}92~\frac{\rm m}{\rm s^2}\approx 4{,}0 ~\frac{\rm m}{\rm s^2},$

$\displaystyle a-A=\frac{3}{10}g=2{,}94~\frac{\rm m}{\rm s^2}\approx 3{,}0 ~\frac{\rm m}{\rm s^2}.$

$\displaystyle b)$ Az $\displaystyle M$ tömegű kiskocsi gyorsulása így is felírható:

$\displaystyle A=\frac{g}{2+\frac{m_1}{m_2}+\frac{M}{m_1}+\frac{M}{m_2}}.$

Látható, hogy

$\displaystyle 0<A<\frac{g}{2} .$

Az $\displaystyle A\approx \tfrac12 g$ felső korlát akkor közelíthető meg, ha $\displaystyle M\ll m_1 \ll m_2$. Ebben a határesetben $\displaystyle F\approx K\approx \frac{1}{2}m_2g$ és $\displaystyle a\approx A$.

Statisztika:

39 dolgozat érkezett.
5 pontot kapott:	Bekes Nándor, Fehér 169 Szilveszter, Fekete Balázs Attila, Magyar Róbert Attila, Mamuzsics Gergő Bence, Marozsák Tóbiás , Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Páhoki Tamás, Pécsi 117 Ildikó, Póta Balázs, Sal Dávid, Varga-Umbrich Eszter.
4 pontot kapott:	Berke Martin, Illés Gergely.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	19 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2017. áprilisi fizika feladatai