 |
A P. 4938. feladat (2017. május) |
P. 4938. Vízszintes talajon kezdetben nyugvó, \(\displaystyle {m=10}\) kg tömegű ládát állandó, \(\displaystyle F=30\) N nagyságú, a vízszintessel \(\displaystyle \alpha=30^\circ\)-os szöget bezáró irányú erővel húztunk. Mekkora utat tett meg a láda, és mekkora lett a sebessége, miután 120 J munkát végeztünk? A csúszási súrlódási együttható \(\displaystyle \mu=0{,}2\).
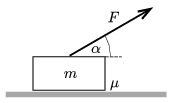
Közli: Holics László, Budapest
(4 pont)
A beküldési határidő 2017. június 12-én LEJÁRT.
Megoldás. A végzett munka
\(\displaystyle W=Fs\cos\alpha,\)
innen a láda elmozdulása:
\(\displaystyle s=\frac{W}{F \cos\alpha}=4{,}6~\rm m.\)
A ládát
\(\displaystyle N=mg-F\sin\alpha=83{,}1~{\rm N}\)
erő szorítja a talajhoz, a súrlódási erő tehát
\(\displaystyle S=\mu N=16{,}6~\rm N.\)
A munkatétel szerint
\(\displaystyle W=\frac{1}{2}mv^2+Ss,\)
ahonnan \(\displaystyle \frac{1}{2}mv^2=43{,}5~\rm J\) és a láda sebessége \(\displaystyle v=2{,}9~\)m/s.
Statisztika:
70 dolgozat érkezett. 4 pontot kapott: Balaskó Dominik, Bartók Imre, Berke Martin, Bíró Dániel, Boros Máté, Bukor Benedek, Csire Roland, Csóka987 Benedek, Csuha Boglárka, Debreczeni Tibor, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Gál Péter Levente, Illés Gergely, Jánosdeák Márk, Jánosik Áron, Keltai Dóra, Kolontári Péter, Kozák András, Krasznai Anna, Mácz Andrea, Magyar Róbert Attila, Makai Enikő, Makovsky Mihály, Mamuzsics Gergő Bence, Markó Gábor, Molnár 957 Barnabás, Molnár Mátyás, Morvai Orsolya, Nagy 555 Botond, Németh Csaba Tibor, Olosz Adél, Ónodi Gergely, Páhoki Tamás, Paulovics Péter, Pécsi 117 Ildikó, Póta Balázs, Pszota Máté, Sal Dávid, Schrott Márton, Szakály Marcell, Tatai Mihály, Tófalusi Ádám, Tóth 111 Máté , Turcsányi Ádám, Varga-Umbrich Eszter, Weisz Máté, Wesniczky Albert, Zöllner András. 3 pontot kapott: 11 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2017. májusi fizika feladatai