A P. 4939. feladat (2017. május)

P. 4939. Az $\displaystyle A$ pontból kilövünk egy golyót, amely a $\displaystyle B$ pontban vízszintesen egy falba ütközik. $\displaystyle B$-ből a $\displaystyle C_1, C_2, \ldots$ pontokba ,,repül'' a golyó, és végül visszajut az $\displaystyle A$ pontba. Az ütközési szám mindenhol $\displaystyle \varepsilon$. Mekkora $\displaystyle \varepsilon$, ha az $\displaystyle A$ pontba érkezés után a golyó már egyáltalán nem pattan fel a talajról?

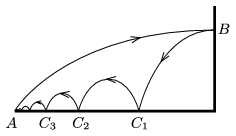
(Feltételezhetjük, hogy a golyóra ható közegellenállási erő elhanyagolható, továbbá a golyó nem jön forgásba.)

Juvancz Gábor (1947–1972) feladata nyomán

(5 pont)

A beküldési határidő 2017. június 12-én LEJÁRT.

Megoldás. Legyen a kilőtt golyó sebességének vízszintes komponense $\displaystyle u_0$, a függőleges komponense pedig $\displaystyle v_0$. A golyó a falat (a $\displaystyle B$ pontot) $\displaystyle t_0=v_0/g$ idő alatt éri el, és

$\displaystyle H=\frac{1}{2}v_0t_0=\frac{v_0^2}{2g}$

magasra emelkedik. Ezalatt

$\displaystyle d=u_0t_0=\frac{u_0 v_0}{g}$

utat tesz meg vízszintesen, ez tehát az $\displaystyle A$ pont és a fal távolsága.

A falról a golyó $\displaystyle \varepsilon u_0$ sebességgel pattan vissza, és ez a vízszintes sebességkomponense a továbbiakban már nem változik. A golyó $\displaystyle t_1=v_0/g$ idő alatt esik vissza a talaj szintjére, vízszintesen tehát

$\displaystyle d_1=\varepsilon u_0t_1=\varepsilon \frac{u_0 v_0}{g}$

az elmozdulása, függőleges sebességének nagysága pedig $\displaystyle v_0$ lesz.

A talajról visszapattanó labda függőleges sebességkomponense $\displaystyle \varepsilon v_0$, a következő pattanásig $\displaystyle t_2=2\varepsilon v_0/g$ idő alatt vízszintes irányban

$\displaystyle d_2=2\varepsilon^2 \frac{u_0 v_0}{g}$

távolságnyit mozdul el.

A további pattanások során a függőleges sebességkomponens mindig az előző érték $\displaystyle \varepsilon$-szorosára csökken, és ugyanilyen arányban csökken a pattanások közötti vízszintes irányú elmozdulás is:

$\displaystyle d_3= 2\varepsilon^3 \frac{u_0 v_0}{g},\quad d_4= 2\varepsilon^4 \frac{u_0 v_0}{g}, \ldots , d_n= 2\varepsilon^n \frac{u_0 v_0}{g}.$

A golyó nagyon sok ($\displaystyle n\rightarrow \infty$) pattanás után, amikor a függőleges sebessége már nullára csökken, visszaérkezik az $\displaystyle A$ pontba. A

$\displaystyle d_1+d_2+d_3+\ldots =d$

feltételből az

$\displaystyle 1=\varepsilon+2\varepsilon^2+2\varepsilon^3+2\varepsilon^4+\ldots=\varepsilon+\frac{2\varepsilon^2}{1-\varepsilon}$

egyenletet kapjuk, amelynek (fizikailag reális, pozitív) megoldása:

$\displaystyle \varepsilon=\sqrt{2}-1\approx 0{,}41.$

Megjegyzés. Ha $\displaystyle \epsilon>\sqrt{2}-1$, akkor a golyó pattogása már az $\displaystyle A$ pontba történő visszaérkezése előtt megszűnik.

Statisztika:

45 dolgozat érkezett.
5 pontot kapott:	Bartók Imre, Bekes Nándor, Bíró Dániel, Bukor Benedek, Csire Roland, Csuha Boglárka, Debreczeni Tibor, Elek Péter, Fekete Balázs Attila, Jakus Balázs István, Jánosik Áron, Kavas Katalin, Kolontári Péter, Kozák András, Krasznai Anna, Makovsky Mihály, Mamuzsics Gergő Bence, Marozsák Tóbiás , Molnár 957 Barnabás, Molnár Mátyás, Morvai Orsolya, Nagy 555 Botond, Ónodi Gergely, Páhoki Tamás, Paulovics Péter, Pécsi 117 Ildikó, Póta Balázs, Szentivánszki Soma , Tófalusi Ádám, Tóth 111 Máté , Turcsányi Ádám, Zöllner András.
4 pontot kapott:	Berke Martin, Édes Lili, Jánosdeák Márk, Olosz Adél, Pszota Máté, Sal Dávid, Varga-Umbrich Eszter.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	3 versenyző.

A KöMaL 2017. májusi fizika feladatai