 |
A P. 4940. feladat (2017. május) |
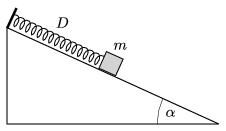
P. 4940. Egy \(\displaystyle \alpha=30^\circ\)-os hajlásszögű, rögzített lejtőn egy \(\displaystyle m=0{,}8\) kg tömegű test az egyik végén rögzített, \(\displaystyle D=30\) N/m direkciós erejű rugóhoz van kötve. A test és a lejtő közötti tapadási és csúszási súrlódás együtthatója egyarányt \(\displaystyle {\mu=0{,}23}\). A testet a rugó nyújtatlan állapotában elengedjük.
\(\displaystyle a)\) Mekkora a test legnagyobb sebessége?
\(\displaystyle b)\) Mekkora a rugó legnagyobb megnyúlása?
\(\displaystyle c)\) Hol áll meg véglegesen a test?
Közli: Zsigri Ferenc, Budapest
(5 pont)
A beküldési határidő 2017. június 12-én LEJÁRT.
Megoldás. A lefelé haladtában \(\displaystyle x\) távolsággal elmozduló test mozgásegyenlete:
\(\displaystyle ma=-Dx+mg(\sin\alpha-\mu\cos\alpha)=-D(x-x_0),\)
ami egy olyan harmonikus rezgőmozgást ír le, amelynek
\(\displaystyle \omega=\sqrt{\frac{D}{m}}=6{,}12~\frac1{\rm s}\)
a körfrekvenciája, egyensúlyi helyzete pedig az indulás helyétől
\(\displaystyle x_0=\frac{mg}{D}(\sin\alpha-\mu\cos\alpha)=7{,}8~~\rm cm\)
távolságra van.
\(\displaystyle a)\) A test legnagyobb sebessége \(\displaystyle x_0\omega=0{,}48~\)m/s.
\(\displaystyle b)\) A rugó legnagyobb megnyúlása \(\displaystyle 2x_0=15{,}6~\)cm.
\(\displaystyle c)\) A \(\displaystyle 2x_0\) megnyúlású rugó által kifejtett erő nem képes felfelé megindítani a testet, hiszen
\(\displaystyle 2Dx_0=4{,}7~{\rm N}<mg (\sin\alpha+\mu\cos\alpha)=5{,}5~{\rm N},\)
ezért a test az első megállása helyén végleg megáll.
Statisztika:
60 dolgozat érkezett. 5 pontot kapott: Balaskó Dominik, Bartók Imre, Bíró Dániel, Bukor Benedek, Csire Roland, Debreczeni Tibor, Fehér 169 Szilveszter, Fekete Balázs Attila, Jakus Balázs István, Jánosdeák Márk, Kolontári Péter, Kondákor Márk, Kozák András, Magyar Róbert Attila, Makovsky Mihály, Mamuzsics Gergő Bence, Molnár Mátyás, Morvai Orsolya, Nagy 555 Botond, Németh 777 Róbert, Németh Csaba Tibor, Olosz Adél, Osváth Botond, Páhoki Tamás, Paulovics Péter, Póta Balázs, Tófalusi Ádám, Tóth 111 Máté , Vajay Mónika, Varga-Umbrich Eszter. 4 pontot kapott: Elek Péter, Illés Gergely, Jánosik Áron, Molnár 957 Barnabás, Ónodi Gergely, Pécsi 117 Ildikó, Sal Dávid, Szentivánszki Soma , Weisz Máté. 3 pontot kapott: 11 versenyző. 2 pontot kapott: 7 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2017. májusi fizika feladatai