A P. 4946. feladat (2017. május)

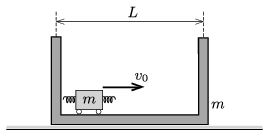
P. 4946. Egy $\displaystyle m$ tömegű kiskocsi szabadon mozoghat egy szintén $\displaystyle m$ tömegű doboz belsejében. A doboz vékony olajréteggel borított asztalon mozoghat, a súrlódási erő csak a doboz sebességétől függ: $\displaystyle {\boldsymbol F=-k\boldsymbol v}$. Kezdetben a doboz áll, a kiskocsi a bal oldali faltól indulva $\displaystyle v_0$ nagyságú sebességgel kezd mozogni jobbra. Hányszor fog rugalmasan ütközni az $\displaystyle \ell$ hosszúságú kiskocsi az $\displaystyle L$ hosszú dobozzal? (A rugalmas ütközést a kiskocsin lévő rugók biztosítják, ezek hossza sokkal kisebb, mint $\displaystyle \ell$.)

A Kvant nyomán

(5 pont)

A beküldési határidő 2017. június 12-én LEJÁRT.

Megoldás. A kiskocsi jobb oldalon ütközik a dobozzal, ekkor ,,sebességet cserélnek''. A doboz lassulva mozog, megtesz $\displaystyle L-\ell$ utat (ha közben meg nem áll), és a bal oldalánál ütközik a kiskocsival. Ekkor a doboz megáll, és a kiskocsi valamekkora $\displaystyle v_1<v_0$ sebességgel elindul jobbra. Ez ismétlődik egészen a doboz megállásáig.

A doboz mozgása szempontjából érdektelenek azok az időtartamok, amikor a doboz áll és csak a kiskocsi mozog, ezeket tehát el is hagyhatjuk, és úgy tekinthetjük, mintha a doboz folyamatosan mozgott volna az

$\displaystyle F= \frac{\Delta(mv)}{\Delta t}=-kv=-k\frac{\Delta x}{\Delta t}$

mozgásegyenlet szerint. Ebből leolvasható, hogy $\displaystyle \Delta(mv(t)+kx(t))=0,$ vagyis az $\displaystyle mv(t)+kx(t)$ mennyiség időben állandó. Mivel kezdetben $\displaystyle v=v_0$, látható, hogy a doboz összesen $\displaystyle s=mv_0/k$ utat tesz meg a megállásáig. (Az ehhez szükséges idő ,,végtelen'' hosszú, mert a sebessége exponenciálisan csökken nullára.) Az ütközések száma

$\displaystyle N=2\left[\frac{s}{L-\ell} \right] +1,$

ahol $\displaystyle [x]$ az egészrész-függvényt ($\displaystyle x$-nél nem nagyobb egész számot) jelöli.

Statisztika:

24 dolgozat érkezett.
5 pontot kapott:	Bekes Nándor, Elek Péter, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Illés Gergely, Kondákor Márk, Kozák András, Krasznai Anna, Marozsák Tóbiás , Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Ónodi Gergely, Osváth Botond, Páhoki Tamás, Szentivánszki Soma , Tófalusi Ádám, Weisz Máté.
4 pontot kapott:	Jakus Balázs István, Sal Dávid.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2017. májusi fizika feladatai