 |
A P. 4953. feladat (2017. szeptember) |
P. 4953. Egy \(\displaystyle A=2~\rm cm^2\) keresztmetszetű, \(\displaystyle L=1\) m hosszú Torricelli-csőbe argongázt juttattunk, ezért benne csak \(\displaystyle h_1=0{,}40\) m magasan áll a higany. A külső légnyomás \(\displaystyle p_0=10^5\) Pa, a kezdeti hőmérséklet \(\displaystyle 20~{}^\circ\)C.
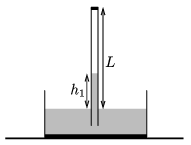
\(\displaystyle a)\) Mekkora tömegű argongáz jutott be a higany fölé?
\(\displaystyle b)\) A gáz hőmérsékletét lassan növeljük. Mekkora a hőmérséklet akkor, amikor a higany magassága a csőben \(\displaystyle h_2=0{,}36\) m?
\(\displaystyle c)\) Mekkora munkát végzett a kitáguló gáz a folyamat során?
Országos Mikola Sándor Fizikaverseny
(5 pont)
A beküldési határidő 2017. október 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Az argongáz nyomása
\(\displaystyle p_1=p_0-\varrho g h_1=4{,}7\cdot 10^4~\rm Pa,\)
térfogata
\(\displaystyle V_1=A(L-h_1)=1{,}20\cdot10^{-4}~\rm m^3.\)
A gáz tömege az egyesített gáztörvény szerint
\(\displaystyle m=\frac{p_1V_1}{RT_1}M=\frac{(4{,}7\cdot 10^4)\cdot (1{,}2\cdot10^{-4})}{8{,}3\cdot 293}\, 40~{\rm g}\approx 93~{\rm mg}.\)
\(\displaystyle b)\) A felmelegített gáz nyomása
\(\displaystyle p_2=p_0-\varrho g h_2=5{,}3\cdot 10^4~\rm Pa,\)
térfogata
\(\displaystyle V_2=A(L-h_2)=1{,}28\cdot10^{-4}~\rm m^3.\)
A megváltozott hőmérséklet a gáztörvény szerint
\(\displaystyle T_2=T_1\frac{p_2V_2}{p_1V_1}=352~\rm K=79\,^\circ\rm C.\)
\(\displaystyle c)\) Könnyen belátható, hogy a gáz nyomása a térfogat változása során lineárisan változik. (Mivel a cső keresztmetszete állandó, a higanyoszlop magassága, ami a külső légnyomás és az argongáz nyomásának különbségével arányos, a higany térfogatával, vagyis a kilógó cső térfogatának és a gáz térfogatának különbségével arányos.) A lineáris \(\displaystyle p(V)\) kapcsolat miatt a munkavégzés számolható a
\(\displaystyle \bar{p}=\frac{p_1+p_2}{2}=5{,}0\cdot 10^4~\rm Pa \)
átlagos nyomásból. Mivel a térfogatváltozás
\(\displaystyle \Delta V= (h_1-h_2)A=8\cdot10^{-6}~\rm m^3,\)
a gáz által végzett munka
\(\displaystyle W=\bar{p}\,\Delta V=0{,}4~\rm J.\)
Statisztika:
114 dolgozat érkezett. 5 pontot kapott: 64 versenyző. 4 pontot kapott: 24 versenyző. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2017. szeptemberi fizika feladatai

