 |
A P. 4957. feladat (2017. szeptember) |
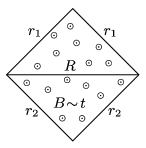
P. 4957. Egy négyzet alakú drótkeret oldalélei az ábrán látható \(\displaystyle r_1\) és \(\displaystyle r_2\) ellenállású huzalokból készültek. A keret az ábra síkjára merőleges, homogén, időben egyenletesen növekvő mágneses indukciójú mezőben van. Mekkora \(\displaystyle R\) ellenállású vezetéket kapcsoljunk a négyzet átlójára, hogy az a leggyorsabb ütemben melegedjen?
Izsák Imre Gyula verseny (Zalaegerszeg) feladata nyomán
(5 pont)
A beküldési határidő 2017. október 10-én LEJÁRT.
Megoldás. A változó mágneses tér miatt az ábrán látható mindkét háromszög oldalai mentén ugyanakkora \(\displaystyle U_0\) körfeszültség indukálódik.

Az ábrán látható jelölésekkel a Kirchhoff-féle huroktörvény egyenletei:
\(\displaystyle RI+2r_1I_1=U_0,\)
\(\displaystyle RI+ 2r_2(I-I_1) =-U_0.\)
Ezekből következik, hogy
\(\displaystyle I=U_0\frac{r_1-r_2}{R(r_1+r_2)+2r_1r_2},\)
az \(\displaystyle R\) ellenállás melegedésének hőteljesítménye:
\(\displaystyle P=I^2R= R\left(U_0\frac{r_1-r_2}{R(r_1+r_2)+2r_1r_2}\right)^2.\)
Ennek a kifejezésnek keressük a maximumát \(\displaystyle R\) függvényében. Mivel \(\displaystyle P(R)\) reciproka így írható fel:
\(\displaystyle \frac{1}{P(R)}=\text{állandó}\cdot \left( R(r_1+r_2)^2+\frac{(2r_1r_2)^2}{R}+\text{állandó}\right),\)
a leggyorsabb melegedés annál az ellenállásnál következik be, amelyre
\(\displaystyle R(r_1+r_2)^2+\frac{(2r_1r_2)^2}{R}\)
minimális. Alkalmazva a számtani és mértani közepekre vonatkozó egyenlőtlenséget azt kapjuk, a \(\displaystyle P(R)\) függvény a maximumát az
\(\displaystyle R=\frac{2r_1r_2}{r_1+r_2}\)
értéknél veszi fel. Ezek szerint akkor melegszik a leggyorsabban a négyzet átlójában található ellenálláshuzal, ha \(\displaystyle R\) az \(\displaystyle r_1\) és \(\displaystyle r_2\) ellenállások harmonikus középértéke.
Statisztika:
14 dolgozat érkezett. 5 pontot kapott: Bíró Dániel, Elek Péter, Fekete Balázs Attila, Kondákor Márk, Marozsák Tóbiás , Olosz Adél, Sal Dávid, Shirsha Bose, Tófalusi Ádám. 4 pontot kapott: Berke Martin. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. szeptemberi fizika feladatai

